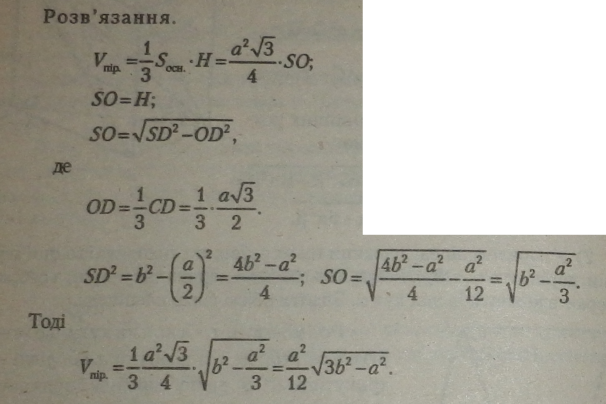Стереометрія. Продовження
Призма. Визначення призми
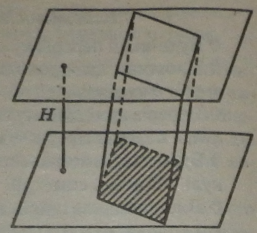
Призмою називається многогранник, який складається з двох пл ских многокутників, що лежать у різних паралельних площинах і су*41 даються паралельним перенесенням, та усіх відрізків, які сполучають відповідні точки цих многокутників. Многокутники називаються основами призми, а відрізки, що сполучають відповідні вершини — бічними ребрами призми.
Бічні ребра призми паралельні й рівні між собою. Поверхня призми складається з основ і бічної поверхні.
Бічна поверхня складається з паралелограмів. Кожний із цих паралелограмів має дві сторони, які є відповідними сторонами основ, а дві інші — сусідніми бічними ребрами.
Висотою призми називається відстань між площинами її основ.
Відрізок, який сполучає вершини призми, що не належать одній грані, називається діагоналлю призми.
Задача.
Бічне ребро похилої призми дорівнює 15 см і нахилене до площини основи під кутом 30е. Знайти висоту призми.
Розв’язання. Висота призми:
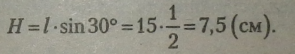
3.1.2. Пряма призма І Визначення прямої і правильної призми
Призма називається прямою, якщо її бічні ребра перпендикулярні до основ. У протилежному випадку призма називається похилою.
Бічні грані прямої призми — прямокутники.
Пряма призма називається правильною, якщо її основи — правильні многокутники.
Площею бічної поверхні призми називається сума площ бічних граней.
Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми (тобто на довжину бічного ребра).

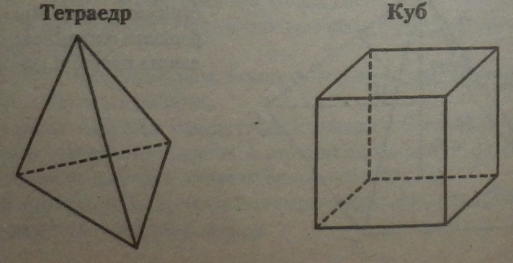
3.2.1. Визначення паралелепіпеда і куба
Паралелепіпедам називається призма, у якої основами є паралелограми.
У паралелепіпеда всі грані — паралелограми.
Протилежні ірані паралелепіпеда паралельні й рівні.
3.2.2. Прямокутний паралелепіпед
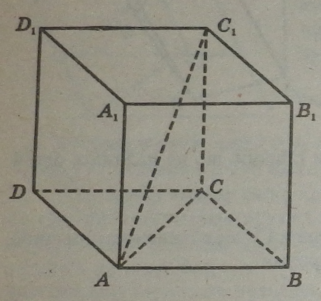
Прямокутним паралелепіпедом називається прямий паралелепіпед основою якого є прямокутник.
Усі грані прямокутного паралелепіпеда — прямокутники.
Довжини непаралельних ребер прямокутного паралелепіпеда називаються його лінійними розмірами.
У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів.
Прямокутний паралелепіпед, усі ребра якого рівні, називається кубом.
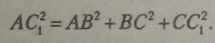
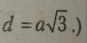
(Якщо довжина ребра куба дорівнює а, то його діагональ
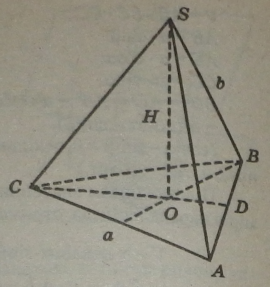
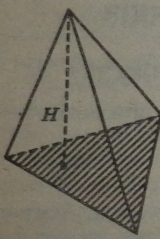
Пірамідою називається многогранник, який складається із плоского многокутника — основи піраміди, точки, що не лежить у площині основи, — вершини піраміди і всіх відрізків, які сполучають вершину піраміди
Відрізки, які сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.
Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань — трикутник, одною з вершин якого є вершина пірамідуа протилежною стороною — сторона основи піраміди.
Висотою піраміди називається перпендикуляр, проведений із вер шини піраміди на площину основи.
Піраміда називається л-кутною, якщо її основа — я-кутник. Трикутна піраміда називається тетраедром.
Площина, яка проходить через вершину піраміди і діагональ основи називається діагональною, а отриманий переріз — діагональним ІSAE).
3.3.2. Властивості елементів правильно! піраміди
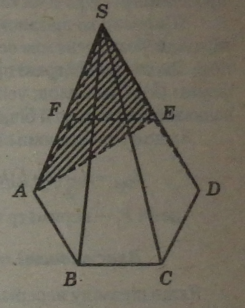
Піраміда називається правильною, якщо її основа — правильний многокутник, і вершина піраміди проецирується у його центр. У правильної піраміди всі ребра рів-ніі і бічні грані — рівні рівнобедрені трикутники.
Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою піраміди.
Якщо позначити сторону основи правильної піраміди через а, а апофему через h, то площа бічної поверхні піраміди:
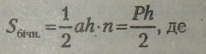
Р— периметр основи піраміди.
Площа повної поверхні піраміди обчислюється за формулою:
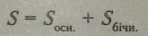
Об’єм піраміди дорівнює одній третині добутку площі и основи 5^ на висоту Я:
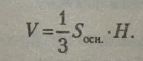
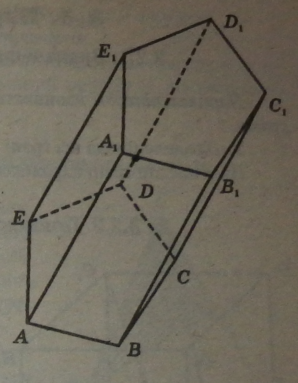
3.3.3. Зрізана піраміда
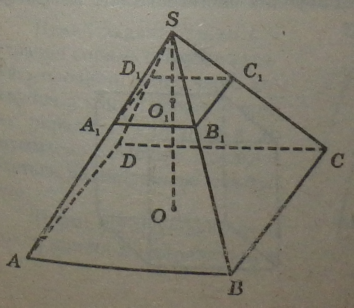
Зрізану піраміду можна отримати, якщо піраміду перерізати площиною, паралельною площині основи.
Зрізана піраміда називається л-кутною, якщо в основі її лежить я-кутник.
Бічні грані зрізаної піраміди — трапеції.
ABCD — нижня основа,
AXBXCXDX — верхня основа.
Висотою зрізаної піраміди називається відрізок перпендикуляра, проведеного з будь-якої точки верхньої основи до площини нижньої.
Правильною зрізаною пірамідою називається частина правильної піраміди, розміщена між основою і площиною перерізу, паралельною основі. Висота бічної грані правильної зрізаної піраміди називається апофемою (А). Сума площ усіх бічних граней (трапецій) зрізаної піраміди називається площею її бічної поверхні.
|
Якщо а і Ь — сторони основ правильної я-кутної зрізаної піраміди, то |
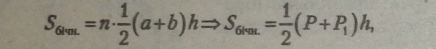 |
|
ДеРіР,- периметр нижньої і верхньої основ. |
Властивості паралельних перерізів піраміди
Якщо піраміду перерізати площиною, паралельною основі, то:
1) бічні ребра і висота поділяються на пропорційні частини;
2) у перерізі вийде многокутник, подібний основі;
3) площі перерізу їхніх основ співвідносяться як квадрати їхніх відстаней від вершини;
4) площина відтинає від піраміди піраміду, подібну даній.
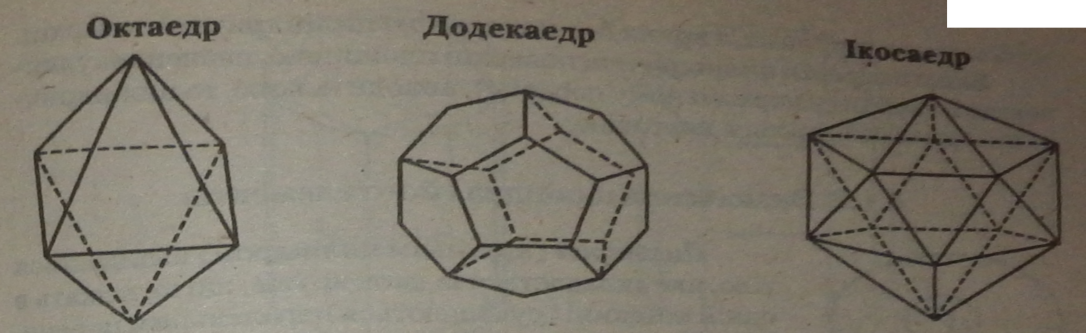
Опуклий многогранник називається правильним, якщо його грані 1 правильні многокутники з однією й тією ж кількістю сторін, а в кожній вершині многогранника сходиться одне й те ж число ребер.
Існує п’ять типів правильних опуклих многогранників: тетраедр, куб, октаедр, додекаедр, ікосаедр.
Правильні многогранники називаються тілами Платона. Об'єми правильних многогранникіе

За Ейлера доводиться, що число правильних
Много гранників не більше п я ти.
4.1.1. Циліндричні поверхні Визначення циліндричної поверхні
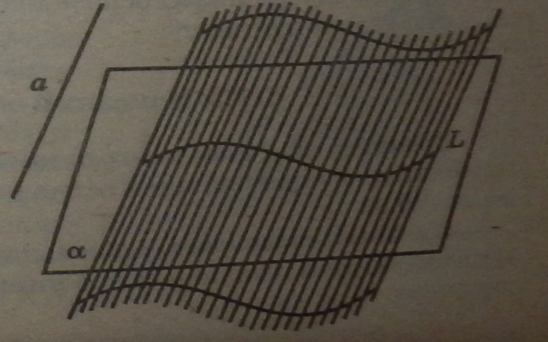
Нехай задана крива І. у площині і пряма а, яка не належить площині. Якщо через кожну точку кривої провести пряму, паралельну прямій а, то отримаємо поверхню, яка називається циліндричною поверхнею.
Прямі, які проходять через точки кривої L і паралельні в,
Називаються твірними, а крива L — напрямною циліндричної поверхні.
Якщо в перерізі циліндричної поверхні площиною, перпендикуляр» ною до її твірної (у нормальному перерізі), виходить коло, то циліндрична поверхня називається круговою.
4.1.2. Визначення циліндра і його елементів
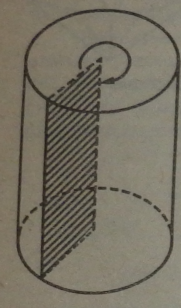
Циліндром (круговим циліндром) називається тіло, яке складається із двох кругів, що не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, які сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, які з’єднують відповідні точки кіл кругів, — твірними циліндра. Ці відрізки утворюють циліндричну поверхню, яка є бічною поверхнею циліндра.
Повна поверхня циліндра складається з основ і бічної поверхні.
Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр наочно можна подати як тіло, отримане в результаті обертання прямокутника навколо сторони як осі.
Радіусом циліндра називається радіус його основи.
Висотою циліндра називається відстань між площинами його основ.
Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.
Переріз циліндра площиною, паралельною його осі, являє собою прямокутник. Дві сторони його — твірні циліндра, а дві інші — паралельні хорди основ. Осьовий переріз циліндра — це переріз площиною, яка проходить через його вісь.
Дотичною площиною до циліндра називається площина, що проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, яка містить цю твірну.
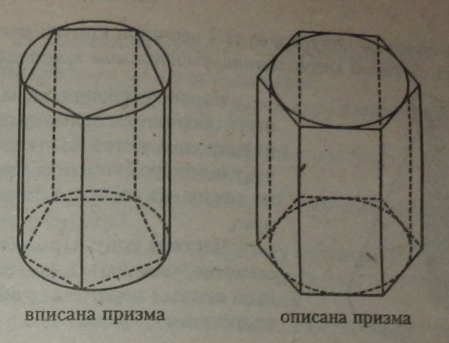
4.1.3. Вписана й описана призми
Призмою, описаною навколо циліндра, називається призма, у якої площинами основ є площини основ циліндра, а бічні грані дотикаються до циліндра.
Призмою, вписаною в циліндр, називається така призма, в якої площинами основ є площини основ циліндра, а бічними ребрами — твірні циліндра. ч
Об’єднання всіх прямих, які про* ходять через кожну точку даної кривої L і деяку фіксовану точку простору S, що не лежить на цій кривій, називається конічною поверхнею.
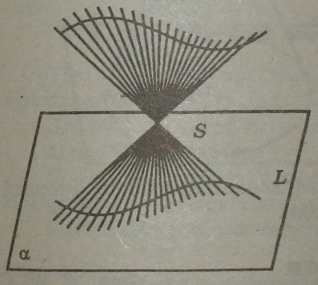
Крива L називається напрямною, фіксована точка S — вершиною, а прямі — твірними конічної поверхні.
Конічні поверхні складаються з двох порожнин із спільною вершиною.
Розглянемо у площині обмежену фігуру D і точку S простору, яка не лежить у даній площині.
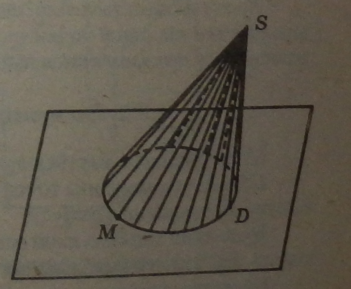
Об’єднання всіх відрізків 5М, де М є D, називається конусом із вершиною в точці 5 і основою D.
Відрізок перпендикуляра, проведеного через вершину конуса до площини основи, називається висотою конуса.
Бічною поверхнею конуса є конічна поверхня, в якої вершина знаходиться у точці S, а напрямною є грани-Ця фігури D.
Якщо основою конуса є круг і вершина конуса проецирується у центр круга, то такий конус називається прямим круговим конусом.
Наочне уявлення про конус можна дістати обертанням прямокутного трикутника навколо одного з його катетів. Тоді гіпотенуза описує бічну поверхню, а катет, що не лежить на осі обертання, — основу конуса.
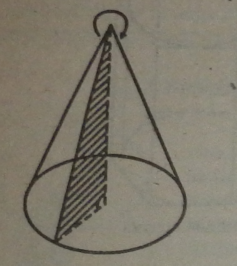
Частина конуса, розміщена між його основою і деякою площиною, яка параде - ; льна основі і перетинає конус, називається зрізаним конусом.
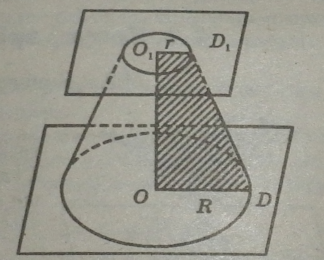
Dx — верхня основа;
D — нижня основа.
Висотою зрізаного конуса називається відстань між площинами основ.
Зрізаний конус, який є частиною прямого конуса, можна дістати обертанням прямокутної трапеції OOxDxD навколо її висоти ООх.
За аналогією з циліндром і призмами вводяться поняття описаної навколо конуса і вписаної в конус піраміди,
4.3.1. Визначення кулі
Кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань — радіусом кулі, і-
4.3.2. Елементи кулі і їхні властивості
Межа кулі називається кульовою поверхнею або сферою.
Сфера — це множина точок кулі, які знаходяться від центра кулі на відстані, що дорівнює радіусу.
Будь-який відрізок, який сполучає дві точки кульової поверхні і проходить через центр кулі, називається діаметром.
Куля, так само як циліндр і конус, є тілом обертання. Вона утворюється обертанням півкруга навколо його діаметра як осі.
Властивості перерізів кулі площинами О Будь-який переріз кулі площиною є круг.
0 Площина, яка проходить через центр кулі, називається діаметральною площиною.
0 Переріз кулі діаметральною площиною називається великим кругом, а переріз сфери — великим колом.
0 Будь-яка діаметральна площина кулі є її площиною симетрії. Центр кулі—її центр симетрії.
0 Площина, яка проходить через точку кульової поверхні і перпендикулярна до радіуса, проведеного в цю точку, називається дотичною площиною, а точка — точкою дотику.
0 Дотична площина має з кулею тільки одну спільну точку — точку дотику.
5.1. Поняття об'єму просторових тіл
Тіло називається простіш, якщо його можна розбити на скінченну кількість трикутних пірамід.
Для простих тіл об’єм — це:
А) величина додатна;
Б) якщо тіло розбите на частини, які є простими тілами, то об’єм цього тіла дорівнює сумі об’ємів його не перекриваючих одна одну частин;
В) об’єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці
5.2. Об'єм прямокутного паралелепіпеда
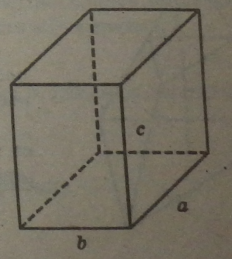
Об’єм V прямокутного паралелепіпеда з лінійними розміри а> Ь, с дорівнює: V •* abc.
5.3. 06'см похилого паралелепіпеда
Єм будь-якого паралелепіпеда дорівнює добутку площі основи на
Два тіла називаються рівновеликими, якщо вони мають рівні об’єми.
Дві трикутні піраміди з рівними площами основ І рівними висотами — рівновеликі.
 |
|
Об’єм призми дорівнює добутку площі її основи на висоту: ~ |
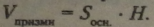
Якщо при перетині двох тіл площиною, паралельною основі (або паралельною заданій площині), площини перерізів однакові, то ці тіла рівновеликі — принцип Кавальєрі.
Об’єм будь-якої піраміди (в т. ч. трикутної) дорівнює одній третині добутку площі її основи на висоту:
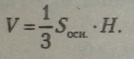
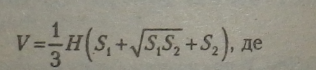
Я — висота зрізаної піраміди; 5, - площа нижньої основи; S2 — площа верхньої основи.
Об’єми двох подібних тіл відносяться, як куби їхніх відповідних лінійних розмірів.
Задачі.
Ї) Обчислити об’єм прямокутного паралелепіпеда, діагональ якого а утворює із площиною основи кут а, а з бічною гранню — кут (3.
Розв’язання. За умовою АС - а; /1CАС - a; Z. ACB - Р - Тоді
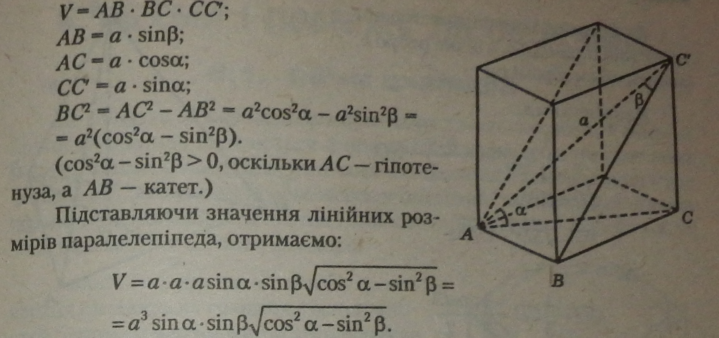
|
2) У паралелепіпеді довжини трьох ребер, які виходять із одної вершини, дорівнюють а, Ь, с. Ребра aib взаємно перпендикулярні, а ребро с утворює з кожним із них кут а. Знайти об’єм паралелепіпеда. |
 |
|
3) Сторона основи правильної трикутної призми до-рівнює а, бічна поверхня рівновелика сумі основ. Знайти об’єм призми. Розв’язання. І |
 |
|
4)-Сторона основи правильної трикутної піраміди а, а бічне ребро Ь. Знайти об’єм піраміди. |
|
|
|
5) У правильній зрізаній чотирикутній піраміді сторони нижньої і верхньої основ дорівнюють а і Ь, а двогранний кут при ребрі нижньої основи дорівнює а. Знайти об’єм піраміди. Розв’язання. |
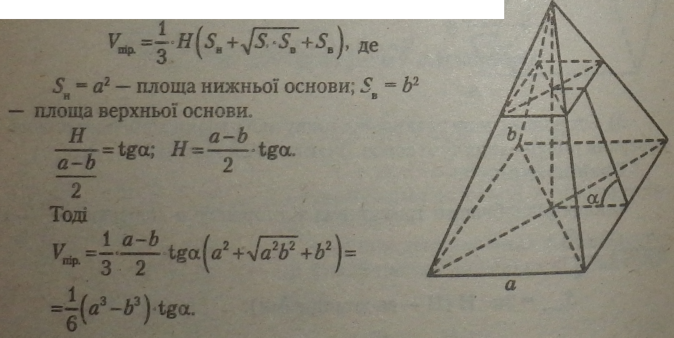 |
Б. ОБ'ЄМИ І ПОВЕРХНІ ТІЛ ОБЕРТАННЯ
До поняття об'єму циліндра приходять таким способом. У прямий круговий циліндр вписуються й описуються навколо нього правильні я-кутні призми, об’єми і поверхні яких обчислюються за наведеними вище формулами. Якщо при необмеженому подвоєнні числа граней призми границя об’ємів як вписаної, так і описаної призм існує, і одна й та ж, то вона називається об'ємом циліндра.
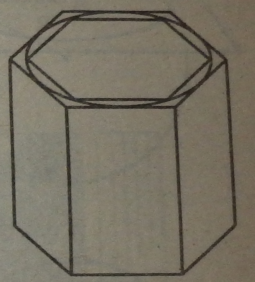
Аналогічно визначається бічна поверхня циліндра як границя послідовностей бічних поверхонь вписаної і описаної призм.
Об’єм циліндра дорівнює добутку площини основи на висоту Я:
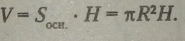
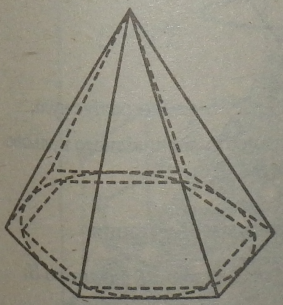
Поняття об'єму конуса вводиться за аналогією з об’ємом циліндра, якщо в конус і навколо нього вписати й описати піраміди, а потім необмежено збільшувати число їхніх граней.
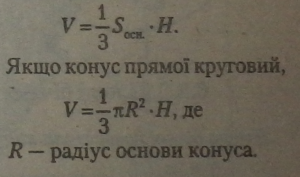
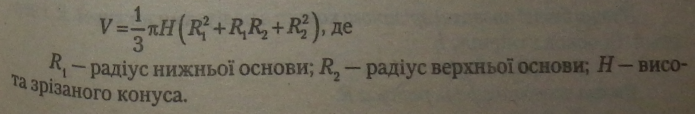
|
6.3.2. Об'єм кульового сектора |
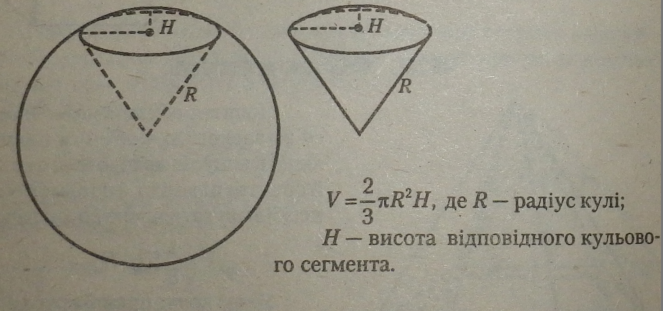 |
6.3.3. Площі бічних поверхонь тіл обертання
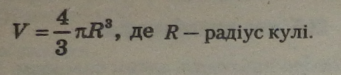 |
|
6.3.1. Об’єм кульового сегмента |
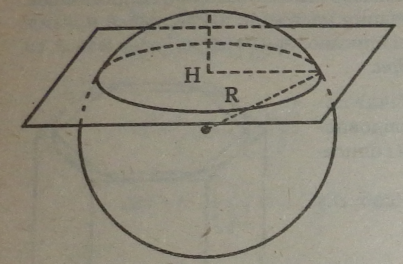
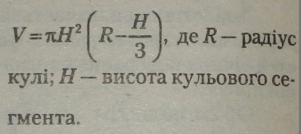
Кульовим сегментом називається частина кулі, яка відсікається від неї площиною.
Площа бічної поверхні циліндра з радіусом основи R і висотою Я:
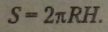
Площа бічної поверхні конуса з радіусом основи R і твірною /:
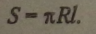
Площа бічної поверхні зрізаного конуса з радіусами нижньої і?, і вЄР* хньої R. основ і твірною /:
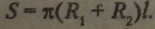 |
|
Площа поверхні сфери радіуса R: |

Автор: admin от 10-06-2013, 19:47, Переглядів: 15303