Стереометрія

Прямі і площини у просторі

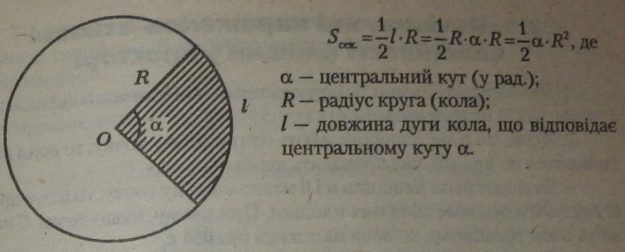
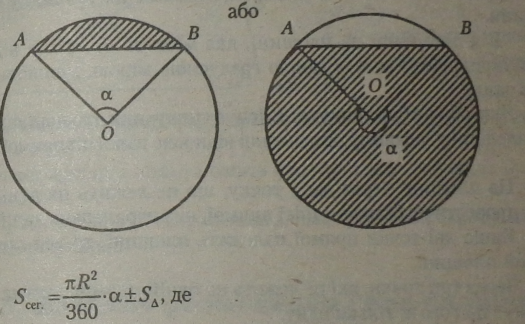
Круговим сегментом називається спільна частина круга і півплощини.

Стереометрія — це розділ геометрії, у якому вивчаються фігури у просторі. Основними фігурами у просторі є точка, пряма і площина.

Позначення: А, В, С, ... — точки; а, b, сЗ — прямі; а, р, — площини.

Аксіоми, які виражають основні властивості площин у просторі

1.  Яка б не була площина, існують точки, які належать цій площині, і точки, які їй не належать.

2.  Якщо дві різні площини мають одну спільну точку, то вони перетинаються по прямій, яка проходить через цю точку.

—  Якщо дві різні площини а і 0 мають спільну точку, то існує пряма с, яка належить кожній із цих площин. При цьому, якщо точка С належить обом площинам, то вона належить прямій с.

3.  Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.

—  Пряма, яка належить площині, розбиває цю площину на дві пів-площини.

—  Від півпрямої на площині, яка містить її, можна відкласти у задану півплощину кут із даною градусною мірою, меншою за 180°, і тільки один.

—  Яким би не був трикутник, існує трикутник, що дорівнює йому, у даній площині у заданому розміщенні відносно даної півпрямої у цій площині.

—  На площині через дану точку, що не лежить на даній прямій, можна провести не більше однієї прямої, яка паралельна даній.

—  Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

—  Через три точки, які не лежать на одній прямій, можна провести площину і до того ж тільки одну.

Взаємне розміщення прямих у просторі

Дві різні прямі у просторі, які мають тільки одну спільну точку, називаються перетпинними.

Дві різні прямі у просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.

Дві прямі, які не перетинаються і не лежать в одній площині, називаються мимобіжними.

Дві різні прямі, паралельні третій прямій, паралельні між собою.

Кут між двома прямими

Дві прямі, які перетинаються, утворюють вертикальні і суміжні кути* Вертикальні кути рівні, а суміжні в сумі становлять 180е. Якщо сумі#*1 кути рівні, то прямі взаємно перпендикулярні. Кут між паралельними прямими вважається рівйим нулю.

Поняття односторонніх, відповідних і різносторонніх кутів при двох прямих і третій січній прямій має місце тільки для прямих, що лежать в одній площині.

Якщо дві прямі, які перетинаються, відповідно паралельні двом іншим прямим, які перетинаються, то кути між ними рівні.

Кут між мимобіжними прямими

Кутом між мимобіжними прямими називається найменший кут між прямими, які перетинаються і паралельні даним мимобіжним прямим.

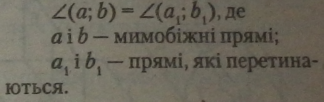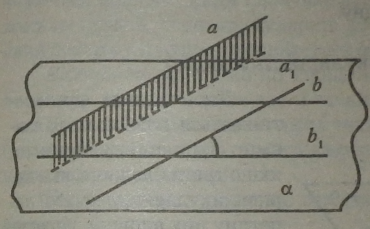
Прямі називаються взаємно перпендикулярними, якщо вони утворюють прямий кут.

Перпендикулярні прямі можуть перетинатися, а можуть бути мимобіжними.

Дві прямі, відповідно паралельні двом перпендикулярним прямим, самі перпендикулярні.

Взаємне розміщення двох площин. Паралельність площин

Дві різні площини, які мають одну спільну пряму, називаються такими, що перетинаються.

Дві площини називаються паралельними, якщо вони не мають спільних точок.

Ознака паралельності площин

Якщо площина паралельна двом прямим, які перетинаються й лежать в іншій площині, то дані площини паралельні.

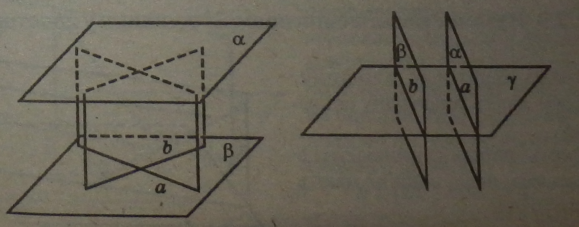
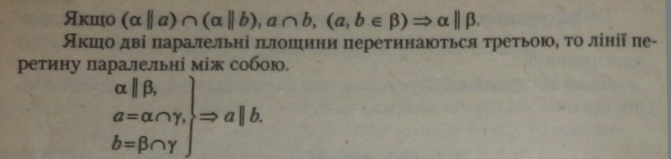Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну.

Перпендикулярність площин

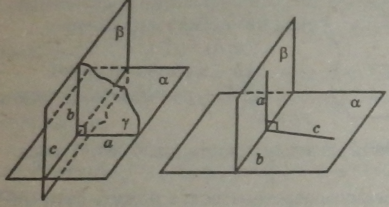Дві площини, що перетинаються, називаються взаємно перпендикулярними, якщо третя площина, яка перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярних прямих.

Ілюстрація означення перпендикулярності й ознаки перпендикулярності площин а і 3.

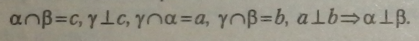Ознака перпендикулярності двох площин

Якщо площина проходить через пряму, перпендикулярну до іншої площини, то ці площини перпендикулярні.

Зад а ча 3. Довести, що існує площина, яка проходить через дану пряму перпендикулярно до даної площини.

Розв'язання. Дано площину а і пряму а. Візьмемо на прямій а точку А і через неї проведемо Пряму b X а. Тоді за ознакою перпендикулярності і наслідком із аксіом (через дві прямі а і Ь, що перетинаються, можна провести площину) будуємо площину р _L а.

Взаємне розміщення прямої і площини у просторі

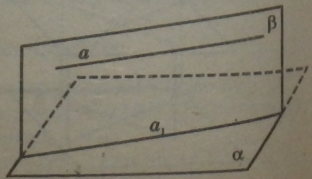
Пряма перетинає площину, якщо вони мають лише одну спільну точку.

Пряма і площина називаються паралельними, якщо вони не мають спільних точок.

Ознака паралельності прямої і площини

Якщо пряма, яка не лежить у площині, паралельна якій - небудь прямій у цій площині, то вона паралельна і самій площині.

Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямо! у площині.

Перпендикуляром, проведеним із даної точки на дану площину, називається відрізок, який сполучає дану точку з точкою площини І лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається основою перпендикуляра.

Відстанню від точки до площини називається довжина перпендикуляра, проведеного із даної точки на площину.

Похилою, проведеною із даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини і не е перпендикуляром до площини.

Кінець цього відрізка, що лежить у площині, називається осноеою похилої.

Відрізок, який сполучає основи перпендикуляра і похилої, проведених із одної точки на площину, називається ортогональною проекцією похилої або проекцією похилої на площину.

Ознака перпендикулярності прямої і площини

Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих, що перетинаються і лежать у цій площині, то вона перпендикулярна до даної площини.

—  Якщо дві прямі перпендикулярні до однієї й тієї ж площини, то вони паралельні.

—  Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.

Теорема про три перпендикуляри

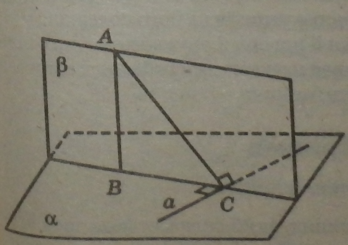
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до і! проекції, то вона перпендикулярна і до само! похилої, і навпаки, якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна й до її проекції.

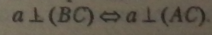
Многогранники

Визначення двогранного кута

Двогранним кутом називається фігура, утворена двома півплощи-нами із спільною прямою, яка обмежує їх. Півплощини називаються гранями, а пряма, яка обмежує їх, — ребром двогранного кута.

Двогранним кутом називається фігура, утворена двома півплощи-нами із спільною прямою, яка обмежує їх. Півплощини називаються гранями, а пряма, яка обмежує їх, — ребром двогранного кута.

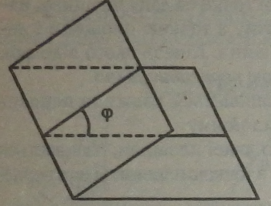
Кут ф називається лінійним кутом двогранного кута — це кут, утворений пів-прямими, отриманими в результаті перетину граней двогранного кута площиною, перпендикулярною до ребра двогранного кута.

За міру двогранного кута приймається міра відповідного йому лінійного кута.

Тригранні кути: нехай а Ь, с — три промені, які виходять із одної точки 5 і не лежать в одній площині.

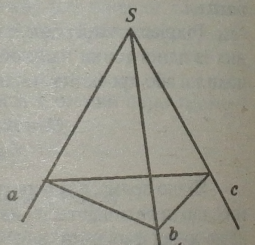
Тригранним кутом (abc) називається фігура, складена із трьох плоских кутів (ab),

(Ьс) і (ас). Ці кути називаються гранями тригранного кута, а їх сторони —ребрами. Спільна вершина плоских кутів називається вершиною тригранного кута.

Двогранні кути, утворені гранями тригранного кута, називаються двогранними кутами тригранного кута.

Якщо із вершини S провести 4,5... променів, то і кути, утворені ними, будуть відповідно чотиригранними, п’ятигранними і т. д. І

Визначення многогранника і його елементів

Многогранник — це тіло, поверхня якого складається зі скінченного числа плоских многокутників.

Многогранник називається опуклим, якщо він лежить з одного боку від площини кожного із плоских многокутників на його поверхні.

Спільна частина такої площини й поверхні опуклого многогранника називається гранню. Сторони граней називаються ребрами многогранника, а вершини — вершинами многогранника.