Рівність трикутників, ознаки рівності трикутників

Ознаки рівності трикутників

В аксіомі 8 (про рівні трикутники) стверджується, що для будь-якого трикутника існує рівний йому трикутник. Використовуючи ознаки рівності трикутників, можна розв’язати обернену задачу: при наявності двох і більше трикутників визначити, чи є серед них рівні трикутники.

Спочатку розглянемо дві задачі на побудову, кута, рівного даному, і трикутника за трьома заданими сторонами.

Задача 1. Дано кут. Побудувати новий кут з такою самою градусною мірою (мал. 31).

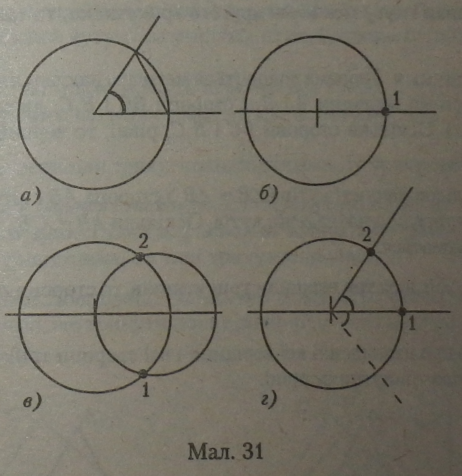
1.  Довільним радіусом з вершини даного кута проведемо коло, що перетинає його сторони (мал. 31, а). Сполучимо точки перетину сторін кута і кола відрізком.

2.  Проведемо горизонтальну пряму (одна сторона нового кута) і відмітимо на ній точку вершини кута (мал. 31, б). З цієї точки тим самим радіусом, що й на мал. 31, а, проведемо коло. Одержуємо точку 1 (точка перетину кола і горизонтальної прямої).

3.  Виміряємо відрізок (мал. 31, а), який сполучає сторони кута в точках його перетину з колом. Радіусом, що дорівнює цьому відрізку, проведемо коло з точки 1 (точка перетину кола і горизонтальної прямої) (мал. 31, в). Точка перетину кіл (точка 2) буде належати другій стороні нового кута.

4.  Сполучимо точку вершини кута і точку 2 (мал. 31, г).

Ми побудували кут, рівний даному, з тою самою градусною мірою.

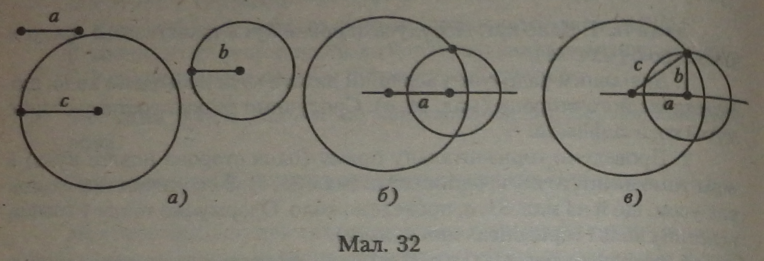
Задача 2. Дано три сторони трикутника. Побудувати трикутник з цими сторонами (мал. 32, а).

1. На горизонтальній прямій відкладемо відрізок а, що дорівнює даному (мал. 32, б). Радіусами кіл, які дорівнюють b і с, із точок кінців відрізка а проведемо кола.

2. Точка перетину кіл в одній ігівплощині є третя вершина трикутника (мал. 32, в). Сполучимо цю вершину з кінцями відрізка а. Одержаний трикутник має сторони, рівні довжинам відрізків а, Ьіс.

Рівність трикутників доводять за сторонами і кутами цих трикутників. Існує три ознаки рівності трикутників.

Розглянемо детальніше кожну з ознак.

Теорема 5 (перша ознака рівності трикутників). Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.

Доведення. Теорема доводиться методом накладення кутів. Сумістимо вершини В і Вх і сторони ВСІ ВХСХ двох трикутників (мал. 33, а). Оскільки сторони В С і ВХСХ рівні, то вершини С і С, теж збігаються.

Внаслідок рівності кутів (ZB = ZBX) сторона ЛВ і сторона А{ВХ повинні збігатися при накладенні кутів. Оскільки АВ — A ХВХ, то вершини А і Ах теж збігаються.

Якщо збіглися три вершини трикутників, то сторони А С і А х Сх збігаються.

Якщо при накладенні всі вершини і всі сторони трикутників збігаються, то такі трикутники рівні

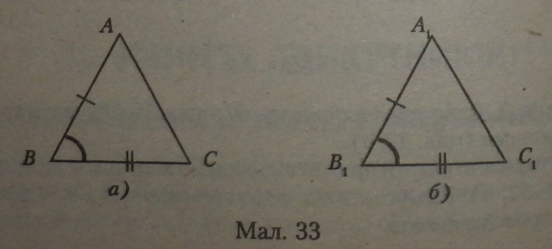Теорема 6 (друга ознака рівності трикутників). Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють аідщнгідяо стороні й прилеглим до не! кутам другого триіутчм, то такі трикутники рівні.

Доведения. Доведення аналогічне доведенню до теореми 5. Застосуємо метод накладення одного трикутника на інший.

Сумістим вершини А і At трикутників (мал. 34, а) так, щоб сторона ЛСзбіглась з напрямком сторони AtCt. Оскільки сторони А Сі А1С1 рівні, то вершина С збігається з вершиною Су.

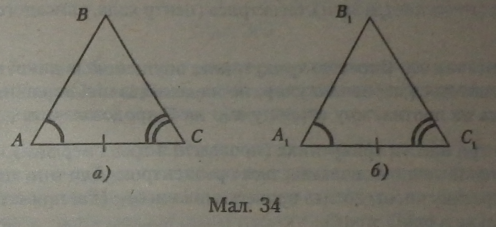
Оскільки кути А і Ах рівні, сторона АВ збігається зі стороною AtBt. Кут С рівний куту С, за умовою, отже, сторона ВС збігається зі стороною BtCv

Оскільки дві прямі можуть перетнутись тільки в одній точці (за означенням прямих, що перетинаються), то вершина В повинна збігтись з вершиною Вх.

Якщо три вершини трикутників збігаються, то трикутники рівні.

Теорема 7 (третя ознака рівності трикутників). Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні.

Доведення. Доведення ведеться методом від супротивного (мал. 35) Припустимо, що трикутники не рівні, тоді в них не рівні відповідн кути (мал. 35, б).

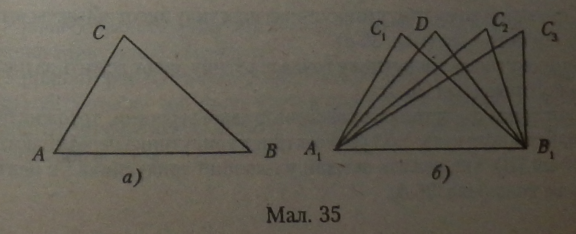
У такого трикутника вершина С, при накладенні трикутників не збігається а вершиною С першого трикутника, а буде знаходитись в якій-нсбудь іншій точці (Cv С% та ін.). З цього витікає, що сторони AXCV AtC3 не будуть рівні стороні АС і сторони ВХСГ ВХС3 не будуть рівні стороні ВС.

Таке припущення суперечить умові теореми, а тому вершина С може збігтись тільки з вершиною Сх.

Висота, медіана і бісектриса трикутника

У трикутника є три головні ліні! і точки: висота (точка ортоцентра), медіана (точка центра ваги), бісектриса (центр кола, вписаного в трикутник).

Означення. Висотою трикутника, опущеною із дано! вершини, називається перпендикуляр, проведений із цієї вершини трикутника на протилежну сторону або на П продовження.

Усі три висоти трикутника (проведені з трьох вершин) перетинаються в одній точці, яка називається ортоцентром. Для того щоб знайти точку перетину висот, досить провести дві висоти (дві прямі перетинаються тільки в одній точці).

Розміщення ортоцентра (точки О) визначається видом трикутника. У гострокутному трикутнику точка перетину висот знаходиться на площині трикутника (мал. 36 а).

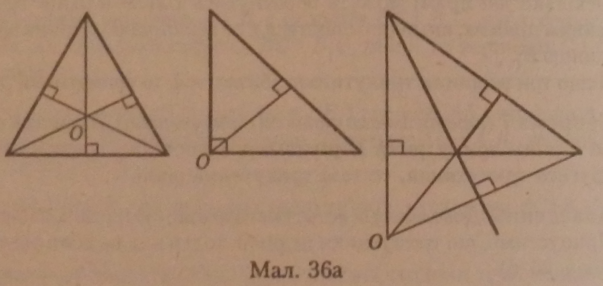
У прямокутному трикутнику точка перетину висот збігається з вершиною прямого кута (мал. 36 а).

У тупокутному трикутнику точка перетину висот лежить за площиною трикутника (мал. 36 а).

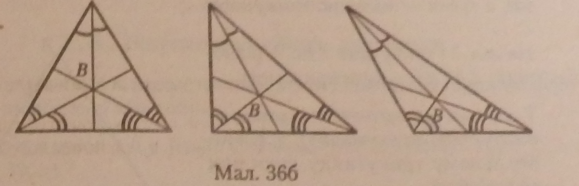
Бісектриса трикутника, проведена із даної вершини, тотожна бісектрисі відповідного кута. Усі три бісектриси трикутника перетинаються в одній точці (В), яка лежить завжди у площині трикутника і є центром вписаного кола (мал. 36 б).

Означення: Бісектрисою трикутника, проведеною із даної вершини, називається відрізок бісектриси кута трикутника, що сполучає цю вершину з точкою на протилежній стороні.

Означення. Медіаною трикутника, проведеною із даної вершини, називається відрізок, який сполучає цю вершину з середи* ною протилежної сторони трикутника.

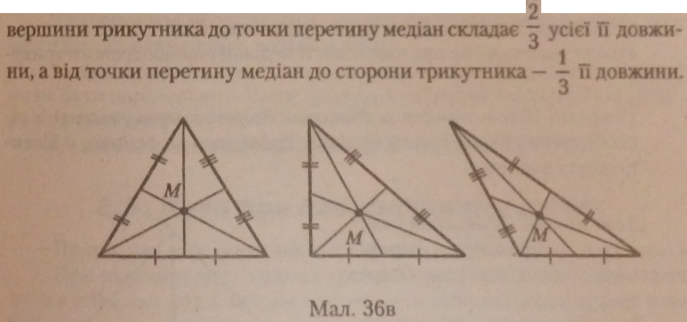
Усі медіани трикутника перетинаються в одній точці (М), яка розміщена на площині трикутника і є його центром ваги. Для знаходження цієї точки достатньо побудувати дві медіани трикутника, і точка їх перетину буде належати третій медіані цього трикутника (мал. 36 в).

Точкою перетину медіан кожна медіана ділиться у відношенні 2:1, рахуючи від вершини трикутника. Тобто довжина відрізка медіани від

У рівнобедреного трикутника медіана, бісектриса і висота, проведені До осцови трикутника, збігаються.

У рівностороинього трикутника всі три лінії (висота, медіана і бісектриса) збігаються і три точки (точки ортоцентра, центра ваги і центра вписаного і описаного кіл) знаходяться в одній точці перетину цих ліній, тобто теж збігаються.

Рівнобедрений трикутник

Означення У рівнобедренного трикутника хоча б дві сторони рівні. Рівні сторони трикутника НАЗИВАЮТЬСЯ бічними сторонами, а третя — основою трикутника.

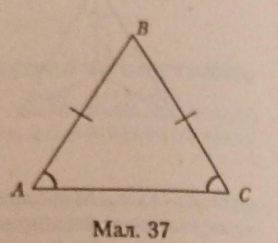
На мал. 37 трикутник ABC — рівнобедреник. ZA і ZC — кути при основі.

Теорема 8 (властивість куттр*б' нобедреного трикутника) У рівно-бедреному трикутнику кути при основі рівні.

Доведення побудоване на теоремі про першу ознаку рівності трнку. тників.

Теорема 9 (оберненадо теореми 8) (озшікарівнобедреного трикутника). Якщо • трикутнику два кути рівні, то вій рівнобедрений.

Доводиться на основі другої ознаки рівності трикутників.

У задачах часто використовується і обернена теорема, коли в трикутнику є рівні кути, але невідомо, що він рівнобедрений.

Розглянемо теорему про властивості медіани рівнобедреного трикутника.

Теорема 10 (властивість медіани рівнобедреного трикутника). У рі-внобедреному трикутнику' медіана, проведена до основи, с бісектрисою і висотою.

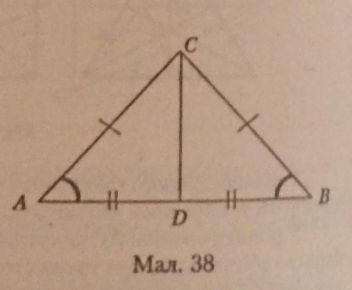
Доведення. Доведення будується на попередній теоремі 8 про рівність кугїв при основі рівнобедре-ного трикутника (мал. 38).

Рівнобедрений МЯСрозбива-ється медіаною CD на два трикутники — ДА CD і ABCD.

Розглянемо АА CD і АВСІ>

АС-СВ, оскільки трикутник АСВ рівнобедрений;

AD - DB, оскільки D — середина відрізка АВ;

Z. CAD - ZCBD — як кути при основі рівнобедреного три кут ник* Отже, AACD - ABCD — за першою ознакою рівності трикуїнии»

Кути при паралельних прямих

Пряма, яка перетинає декілька прямих, називаться січною.