Основні геометричні фігури і їх властивості

Точка, пряма, відрізок, площина. Основні аксіоми геометрії

Геометрія — це наука про властивості геометричних фігур, вона вивчає форму предметів навколишнього світу. Геометрія виникла у зв’язку з потребою у вимірюванні земельних ділянок.

Вивченнягеометрії починається з планіметрії. Планіметрія — це розділ геометрії, який вивчає фігури, розташовані в одній площині.

Найпростішою фігурою на площині є точка. Вона характеризується тільки своїм розміщенням. Усі інші фігури складаються з точок. Точка позначається великою латинською буквою.

Як і точка, однією з найпростіших фігур є пряма. Пряма нескінченна. На малюнку ми можемо зобразити лише її частину. Прямі позначав ються маленькими латинськими буквами. Побудова і властивості більш складних фігур основані на аксіомах. Усього в планіметрії дев’ять ак-сіом.  • . _

Аксіома 1 (властивості приналежності точок і прямих на площині)о Яка б не була пряма, існують точки, які належать цій прямій, і точки, що їй не належать. Через будь-які дві точки можна провести пряму, і тільки одну.

Якщо точка належить прямій (мал. 1), то короткий запис такий: Аеа (читається так: «точка А належить прямій я»). Якщо точка не належить прямій, то короткий запис такий: В е а (читається так: «точка В не належить прямій а>).

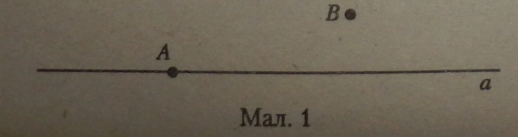
Якщо взяти дві точки, які не збігаються (А і С), то через них можна провести тільки одну пряму (а), хоча через кожну з цих точок можна провести безліч прямих (мал. 2).

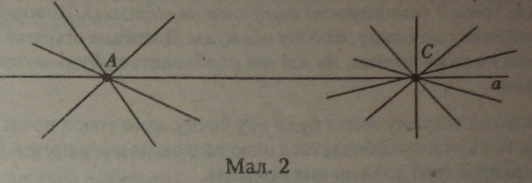
Якщо точки А і С збігаються (на кресленні в цьому випадку одна точка буде позначена двома буквами), то через них можна провести теж безліч прямих.

Аксіома 2 (властивість розміщення точок на прямій). З трьох точок, розміщених на одній прямій, одна і тільки одна лежить між двома Іншими о

Дано три точки: А, В, С.

Можливі варіанти розміщення трьох точок на прямій показані на малюнку 3.

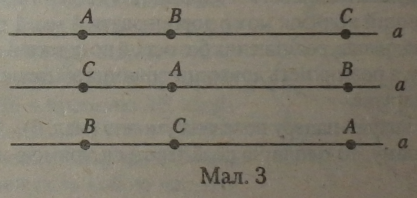
У першому варіанті — В лежить між А і С на прямій а; у другому варіанті—А лежить між Сі В на прямій а у третьому варіанті — С лежить між ІЗ і А на прямій а. Інших варіантів бути не може.

Відрізком називається частина прямої, яка складається з усіх точок цієї прямої, що лежать між двома даними її точками.

Ці дані точки називаються кінцями відрізка і служать для його позначення (мал. 4).

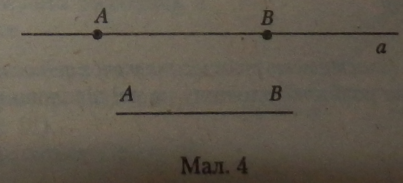
Відрізок ЛіВлежитьнапрямійаіПОЗначаєтьсятжкЛВ є а. Він обмеженні точкою початку відрізка (точкою Д)4 точкою кінця відрізка (то*» кою 5).

Аксіома 3 (властивості вимірювання відрізків). Кожний відріаок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частая, на які він розбивається будь-якого його точкою.

Якщо на відрізку взяти будь-яку точку, крім точок початку і кінця відрізка, то відрізок розбивається цією точкою на два відрізки і його довжина дорівнює сумі довжин цих відрізків.

Відрізок АВ точкою С розбитий на два відрізки (АСіСВ Довжина відрізка ДО дорівнює сумі довжин відрізків А С і СВ: АВ — АС+СВ.

Довжина кожного з одержаних відрізків дорівнює різниці довжин цілого відрізка (АВ) і його другої частини (СВ або АС).

АС-АВ-СВ і СВ-АВ-АС Довжина відрізка вимірюється в одиницях довжини метричної системи мір. Одиничний відрізок може дорівнювати 1 мм, і см і т. д. Кількість одиничних відрізків, розміщених без остачі по довжині відрізка, складає його довжину, а розмірність довжини повинна збігатися з розмірністю одиничного відрізка.

Площина на аркуші паперу показана умовно (мал. 6). Якщо на площині провести пряму, то площина розбивається прямою на дві півпло-щини (мал. 7).

Аксіома 4 (властивість розміщення точок відносно прямої на пл° щині). Пряма розбиває площину на дві півплощини.

Промінь. Кут і його градусна міра

Аксіоми 5, б, 7

Я мжо на премій в ю*тмтечЕуЛ, тоіія точ карг/Уж н.*/ пряму па яА піапряміа, tu2 (ш.&).

Півпрямі <ft і аг е променями.

Премія» (або півпряма) — це частина прямої яка складається з усіж точок цієї прямої, що лежать по оту сторону від даної А точхиі мйВМЦІ що точку. Ця точка називається почтовою точко« пІі«фш^^ВмЄ' ' ня).

Позначається промінь дика точками: початковою точкою і якою точкою на цьому промені. Э однієї точки можна про* иескім-ченну множину променів. На промові можна відкласти да» точку* крім вершини променя, яка буде належати Вирізку, якаА здшводрш му промені

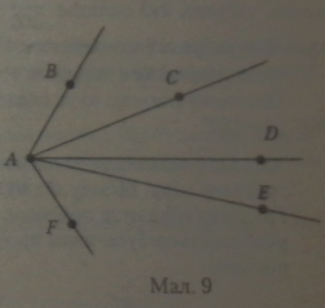
З точки А на малюнку проведено п’ять променів: АВ, AC, AD, АЕ і AF. На кожному промені відкладено відрізок, який йому належить: відрізок АВ є променю АВ, відрізок АС є променю АС, відрізок AD є променю AD, відрізок АЕ є променю АЕ, відрі-зок AFe променю AF.

Два промені, які виходять з однієї точки, обмежують собою частину площини, яка розташована між променями. Фігура,, яка при цьому утво-рюється, називається кутом. Промені із спільною вершиною в точні початку променів називаються стартами кута. Вершина кута розміщена в точці початку променів.

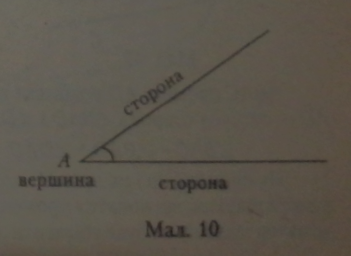
Означення. Кут — це части-: на площини, обмежена двома променями, які виходять з однієї точки.

Кут — це геометрична фігура, яка має вершину» сторони і свою градусну міру (мал. 10).

Кути вимірюються в градусах.

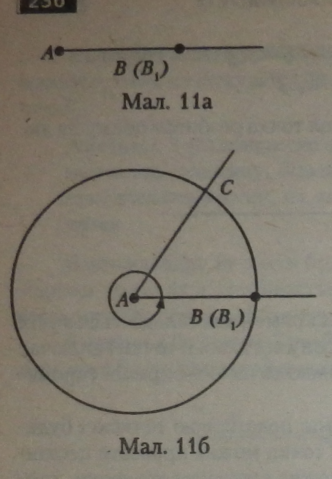
Розглянемо кут, сторони якого збігаються (Z2M2?,). Його градусна міра дорівнює 0* (мал. 11 а).

Якщо одну сторону кута (АВ) закріпити, а другу сторону (АВ{) обертати проти годинникової стрілки доти, доки вона не співпаде з першою стороною (AS), то площина такого кута складе повний кут (мал. 11 б). Отже, кут А (позначається ZA) — повний кут.

Кути позначаються так: 1) значок кута перед буквою, яка розташована у вершині кута (наприклад ZA); 2) значок кута перед трьома буквами, середня з яких належить вершині кута (наприклад ZBA С); 3) значок кута із зазначенням сторін кута (наприклад Zab).

Якщо взяти повний кут і розділити його на 360 частин (кутів), то

Кожна частина, яка складає TjgQ частину повного кута, називається

Кутовим градусом (позначається 1°).

Отже, повний кут дорівнює 1* • 360 * 360е.

Половина повного кута складає розгорнутий кут, який дорівнює 360е: 2 - 180е.

Аксіома 5 (властивості вимірювання кутів). Кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут дорівнює 180°. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.

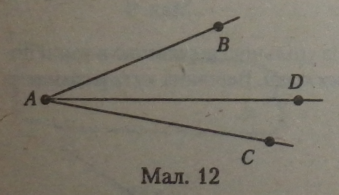
Якщо з вершини кутаЛ провести ще один промінь AD, який проходить між сторонами кута, то кут розбивається цим променем на два кути, в яких одна сторона (промінь AD) буде спільною, а дві інші — сто-рони заданого кута (мал. 12).' ZBAC промінь AD розбиває на два кути: ZBAD і ZDAC. Промінь AD — спільна сторона ZBAD і ZDAC. Отже, за аксіомою 5:

ZBAC - ZBAD +. ZDAC.

На промені, як і на прямій, можна відкладати відрізки. Можна від* класти відрізок від початку променя, а можна відкласти відрізок так, Ш° початок відрізка не буде збігатися з початком променя (мал. 13).

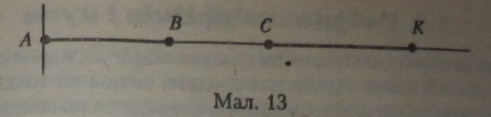
Відрізок АВ на промені А відкладений від точки початку променя, а відрізок СК відкладений на промені.

Якщо ми візьмемо не промінь, а пряму (мал, 14), то відрізок довжини АВ ми можемо відкласти в дві півплощини, на які розбиває площину пряма, що проходить через точку А (АВ ш АВХ т АВ2). Цього не можна зробити на промені, оскільки він направлений тільки в одну сторону (розміщений в одній півплощині від точки А).

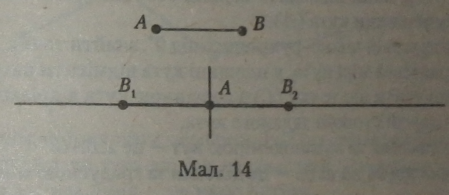
Аксіома 6 (властивість відкладання відрізків). На будь-якій пів-прямій від її початкової точки можна відкласти відрізок даної довжини, і тільки один.

Аксіома 7 (властивість відкладання кутів). Від будь-якої пшпря-мої у дану півплощину можна відкласти кут із даною градусною мірою, меншою за 180°, і тільки один.

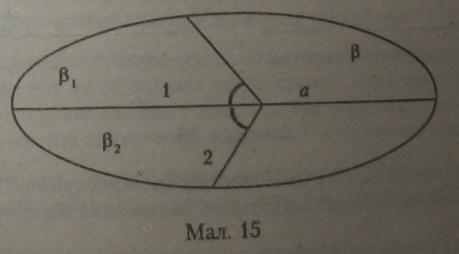
Zl - Z2 - 60°, кути розміщені у різних півплощинах відносно прямої я, але в одній площині р (мал. 15).