Трикутник

Означення. Два і більше відрізків прямих, розміщені під кутом один до одного так, що початок кожного наступного відрізка сполучається з кінцем попереднього відрізка, складають ламану лінію. Кожний відрізок ламаної лінії називають ланкою ламаної лінії.

Ламана лінія — це геометрична фігура, що складається з точок і відрізків, які сполучають їх. На малюнку 17 триланкова незамхнеш ламана лінія, у якої початок першого відрізка не сполучено з кінцем останнього відрізка.

Якщо у ламаної початок першого відрізка сполучається з кінцем останнього відрізка, то така ламана називається замкненою ламаною. Замкнена ламана лінія — це многокутник.

Означення. Многокутник — це геометрична фігура, обмежена замкненою ламаною лінією, ланки якої не лежать на одній прямій.

Многокутник — це плоска геометрична фігура, що має вершини (сполучаючі точки кінця одного відрізка і початку наступного відрізка ламаної), сторони (відрізки, або ланки, ламаної), кути (частина площини біля вершини, розташована між двома ланками ламаної, що розміщені одна за одною) і діагоналі (відрізки прямих, що сполучають дві не сусідні вершини многокутника, який має більше трьох ланок). Триланкова замкнена ламана лінія — це трикутник.

Означення. Трикутник — це плоска геометрична фігура, що має три точки, які не лежать на одній прямій, і три відрізки, котрі сполучають ці точки. Три точки — це три вершини трнкулшка, а три відрізки, що сполучають вершини, — це сторони трикутника.

Трикутник має три кути, вершини яких сполучаються з вершинами трикутника, а сторони кутів — це пари поряд розміщених сторін трикутника.

Види трикутників визначають за довжиною їх сторін і за величинами кутів трикутника.

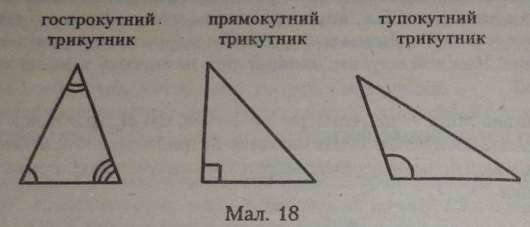
Залежно від величин кутів трикутники діляться на:

— гострокутні (всі три кути трикутника гострі);

Рівносторонній трикутник є рівнобедреним.

Сума сторін трикутника називається периметром довжин.

—  прямокутні (один кут — прямий); —  тупокутні (один кут — тупий)

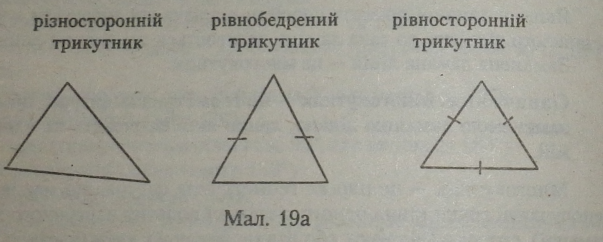
Залежно від довжин сторін трикутники діляться на: —різносторонні (всі сторони різної довжини); —рівнобедрені (хоч би дві сторони мають однакову довжину); —рівносторонт (yd сторони однієї довжини) (мал. 19 а).

Якщо сторони трикутника позначити буквами а, Ь, с, а периметр буквою Р, то формула для обчислення периметра будь-якого трикутника (див. мал. 19 б) така:

Р*=а + Ь + с

Формула обчислення периметра рівнобедреного трикутника, у якого сторони аіс рівні, спрощується:

Р~2а + Ь

Для рівностороннього трикутника, у якого всі сторони рівні, периметр визначається за формулою:

Р-За

Якщо довжини сторін трикутника виражені різними одиницями вимірювання, то їх спочатку треба звести до однієї одиниці вимірювання, а потім додати.

Розглянемо приклад розв’язування задачі на обчислення периметра даного трикутника. Довжини сторін трикутника позначимо маленькими латинськими буквами.

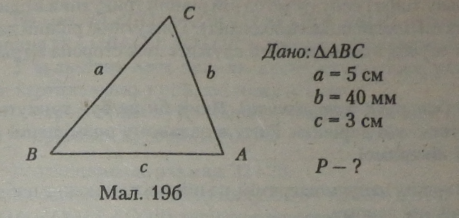
Розв’язання.

Периметр трикутника: Р і а + b + с.

Запишемо довжину сторони | у тих самих одиницях виміру, що і дві інші сторони: b = 40 мм — 4 см.

Підставимо числові дані в формулу периметра й обчислимо: Р • 5 + 4 + 3 = 12 (см).

Відповідь: 12 см.

V Трикутник можна побудувати тоді, коли ламана триланкова крива буїде замкнена, а для цього треба, щоб сума довжин будь-яких ланок ламаної була більшою за довжину третьої ланки.

Існування трикутника, рівного даному

Означення. Трикутники називаються рівними, якщо у них відповідні сторони і відповідні кути рівні. -

У рівних трикутників проти відповідних сторін лежать відповідні кути.

На мал. 20 подані рівні трикутники, але по-різному орієнтовані на площині. Ж

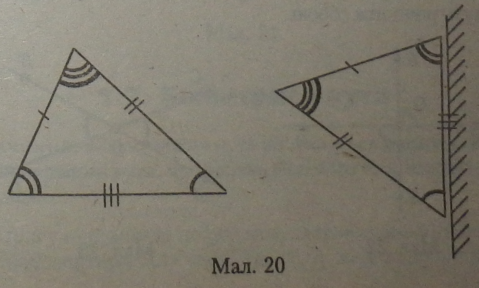
У рівних трикутників периметри теж рівні.

На мал. 20 трикутнику, розміщеному ліворуч, основою служить горизонтальна пряма (сторона трикутника з трьома штрихами). Тепер візьмемо вертикальну лінію і побудуємо на ній рівний трикутник в одній з пі в Площин (друга півплощина заштрихована). Трикутник, рівний даному, побудований справа, і основою його служить теж сторона з трьома штрихами.

Аксіома 8 (про рівні трикутники). Який би не був трикутник існує трикутник, що дорівнює йому в заданому розміщенні від. носно даної півпрямоі.

Задавши будь-який напрямок прямій, на ній завжди можна побудувати трикутник, рівний даному.