Квадратні рівняння
Повні і неповні квадратні рівняння

Числа а, b і с — коефіцієнти квадратного рівняння: а — перший коефіцієнт, Ь — другий коефіцієнт, а с— вільний член рівняння.
Квадратне рівняння — це рівняння другого степеня, бо в його лівій частині стоїть многочлен другого степеня.
Якщо в рівнянні стоїть квадратний тричлен ах1+ Ьх+ + с, то рівняння повне. Якщо відсутній один або два з одночленів, але одночлен другого степеня зберігається, то таке рівняння називається неповнимквадрат* шш рівнянням.
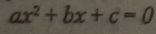 |
|
загального виду. |
— повне квадратне рівняння, або квадратне рівняння
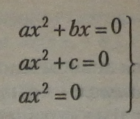
Розв’язування рівняння — це одержання чисельних значень (коренів) х{і х2(два корені, оскільки вищий степінь рівняння визначає кількість його коренів), які перетворюють рівняння у правильну числову рівність.
Розв’язування неповних квадратних рівнянь Правило. Розв'язування неповного квадратного рівняння виду
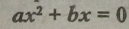
здійснюється за допомогою винесення спільного множника (*) за дужки.
Добуток одночлена і многочлена, які містять невідоме, дорівнює нулю, коли хоча б один із множників дорівнює нулю.
вимагає виділення дг у ліву частину рівняння і добування квадратного кореня.
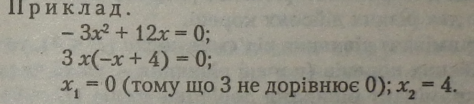 |
|
Правило. Розв’язування неповного квадратного рівняння виду |
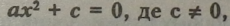
|
Приклад. |
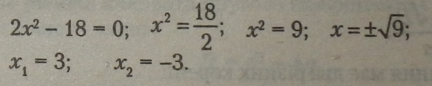 |
Правило. Неповне квадратне рівняння виду лх2 = 0 має два однакових корені xt = х2 - 0.
Приклад.
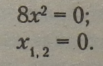
3.2. Розв'язування повного квадратного
Повне квадратне рівняння має вигляд:
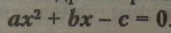
При розв’язуванні повного квадратного рівняння можливі три варіанти:
1) рівняння має два різних корені*
2) рівняння має два однакових корені;
3) рівняння не має дійсних коренів.
Вибір одного з трьох варіантів визначається знаком многочлена Ь1 — 4ас.Вираз Ь2 - 4ас називається дискримінантом і позначається великою латинською буквою «де» (D). У перекладі на українську мову «дискримінант» означає «розрізняючий».
Пра вило. Дискримінант рівняння дорівнює різниці квадрата другого коефіцієнта і збільшеного вчетверо добутку першого ко* ефідієнта і вільного члена.
Формула визначення дискримінанта:
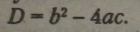
Дійсно, для розв’язування квадратного рівняння порівняння дискримінанта з 0 дає відповіді на запитання:
1) чи має рівняння корені (чи є вони дійсними числами);
2) скільки коренів має рівняння.
Правило. Якщо дискримінант рівняння додатне число (D > 0), то рівняння має два різних дійсних корені.
Якщо дискримінант рівняння від'ємне число (D < 0), то рівняння не має дійсних коренів (корені рівняння — уявні числа).
Якщо дискримінант рівняння дорівнює нулю (D = 0), то рівняння має два однакових корені.
Дискримінант використовується у формулі обчислення коренів повного квадратного рівняння.
Формула для обчислення коренів повного квадратного рівняння:
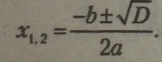
|
При D > 0 рівняння має два різних корені: |
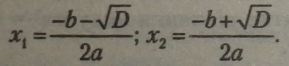 |
|
При D - 0 рівняння має два однакових корені: |
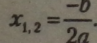
При D < 0 рівняння дійсних коренів не має.
Зведене квадратне рівняння
Якщо перший коефіцієнт повного квадратного рівняння дорівнює 1, то таке рівняння називається зведеним квадратним рівнянням.
Означення. Зведене квадратне рівняння — це повне квадратне рівняння, у якого перший коефіцієнт дооівнює 1. Загальний вигляд зведеного квадратного рівняння:
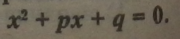
Порівняємо загальний вигляд повного і зведеного квадратних рівнянь:
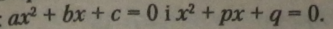
Букви коефіцієнтів зведеного квадратного рівняння не збігаються з буквами повного квадратного рівняння, тому слід значення коефіцієнтів зведеного квадратного рівняння узгодити з коефіцієнтами повного квадратного рівняння.
Для відповідності коефіцієнтів поділимо другий коефіцієнт і вільний член повного рівняння на його перший коефіцієнт:
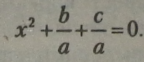
|
З цього виходить, що |
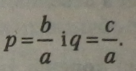 |
Розв’язування зведеного квадратного рівняння має ту саму методику, що й повного. Спочатку визначається дискримінант, а корені рівняння обчислюються через коефіцієнт і вільний член за формулами:
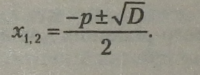
Правило. Корені зведеного квадратного рівняння дорівнюють половині виразу, що складається із другого коефіцієнта, взятого з протилежним знаком, плюс-мінус корінь із дискримінанта.
Розглянемо дискримінант зведеного квадратного рівняння.
Пр авило. Дискримінант зведеного квадратного рівняння дорівнює різниці квадрата другого коефіцієнта і збільшеного вчетверо вільного члена:
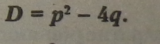
Якщо D > 0, то рівняння має два різних корені.
Якщо D < 0, то рівняння не має дійсних коренів.
Якщо D - 0, то рівняння має два однакових корені.
^ Повне квадратне рівняння не завжди доцільно переводити у зведене (наприклад, якщо коефіцієнти зведеного рівняння — дробові числа), але, в принципі, завжди можна з повного квадратного рівняння одержати зведене квадратне рівняння.
Приклад.
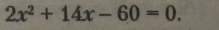
Оскільки є спільний множник (2), переведемо повне рівняння у зведене:

|
Обчислимо дискримінант за формулою: |
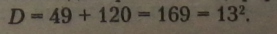 |
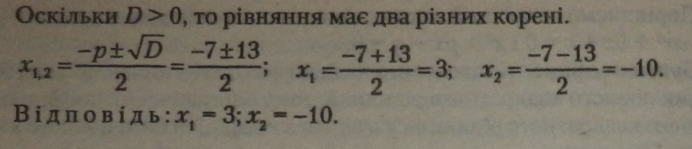
У зведеному квадратному рівнянні властивості коренів описані теоремою Вієта. Ця теорема застосовується для обчислення коренів зведеного квадратного рівняння з невеликими числовими значеннями коефіцієнтів, які можна швидко обчислити методом підстановки.
Теорема (Вієта). Сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, тобто
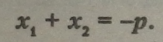
Добуток коренів зведеного квадратного рівняння дорівнює його вільному члену, або
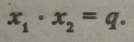
Зведене рівняння перевіряється дискримінантом на кількість коренів рівняння.
Якщо D > 0, то рівняння має два корені і може бути розв’язане за теоремою Вієта.
Якщо D < 0, то рівняння не має коренів, теорема Вієта не працює. При D = 0 у рівняння два однакових корені, у цьому випадку теорема Вієта може читатися так:
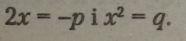
Приклад.
Розв’яжіть зведене квадратне рівняння за формулами Вієта.

Обчислимо дискримінант за формулою для зведеного рівняння:
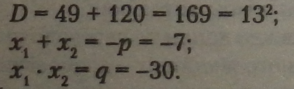
Підберемо два числа, сума яких дорівнює -7, а добуток дорівнює
Якщо сума коренів — від’ємне число, то обидва корені — від’ємні числа або один корінь — від’ємне число (більше), а другий — додатне число (менше).
Оскільки добуток двох чисел зі знаком «-», то корені рівняння ма-. ють різні знаки.
Виходячи з такого аналізу, ми говоримо, що два корені мають різні знаки і більший за числовою величиною корінь у рівняння — від’ємник.
Отже, пара чисел (-10) і 3 задовольняє цю умову рівняння повніс-х в -10 і х2 - 3 є розв’язком зведеного рівняння Xі+ їх - ЗО - 0. Відповідь:*, - 3;х2--10.
Теорема, обернена до теореми Вієта, необхідна для того, щоб за заданим значенням двох коренів скласти зведене рівняння.

Теорему Вієта використовують для перевірки знаків коренів при обчисленнях; при визначенні одного з коренів, якщо задане зведене рівняння і другий корінь; для перевірки правильності розв’язання зведеного рівняння за його формулами.
3.5. Розв'язування раціональних рівнянь, які приводять до квадратних рівнянь
У практичній алгебрі часто обчислюються рівняння зі степенями вище двох, які простіше розв’язувати за формалізованим способом розв’язування квадратних рівнянь.
Означення. Рівняння, зведені до квадратних, — це рівнянні степенів вище двох, які можна замінити на квадратні рівняння вводячи нову змінну. Кожне таке рівняння вимагає свого конк ретного способу перетворення.
Приклади.
1. Розв’язати біквадратне рівняння (квадратне рівняння відносн квадрата невідомого):
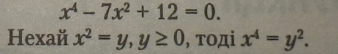 |
|
Перепишемо рівняння з новим невідомим у: |
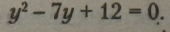
|
Обчислимо дискримінант одержаного рівняння: |
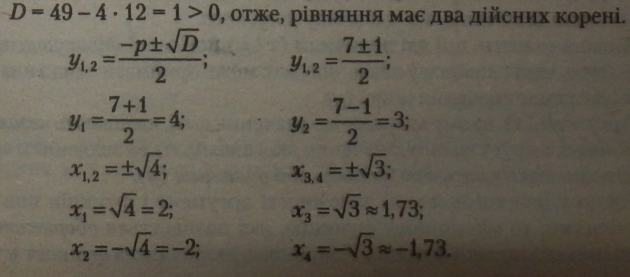 |
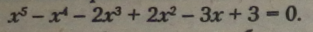
|
Перетворимо рівняння способом групування і винесення спільного множника за дужки: |
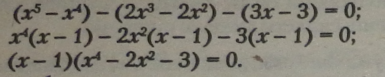 |
|
Якщо добуток двох співмножників дорівнює V, то хоча бодин ІЗ співмножників дорівнює 0: |
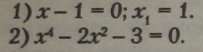
Біквадратне рівняння заміною змінної переведемо у зведене квадратне рівняння. Нехай
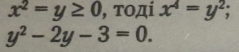
|
Обчислимо дискримінант і визначимо корені одержаного квадрат* ного рівняння: |
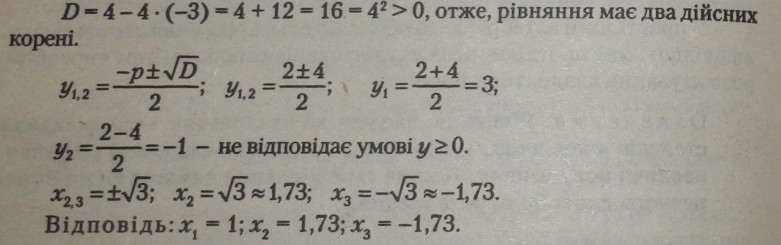 |
4.1. Аргумент і числове значення функції
Функція з латинського перекладається, як «виконання», «діяльність*, тому що вона є залежною величиною, яка змінюється разом із зміною іншої величини, що має назву аргумент.
Можна сказати, що дві величини (х і у) пов’язані функціональною залежністю, якщо кожному значенню, яке може приймати одна з них (х), відповідає єдине значення іншої (у).
Аргумент (х), якому ми надаємо значення самі, називають незалеЖт ною змінною, а другу змінну, значення якої знаходять за значенням аріу* менту, називають залежною змінною або функцією (у).
Якщо у функціональній залежності аргумент і функція помінялись місцями, то маємо нову функцію, яка називається оберненою по відношенню до заданої функції. Наприклад, якщо задана функція
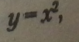
функції. ’
Функцію можна задавати словесно, таблицею (табличний спосіб задавання функції), графіком (графічний спосіб задавання функції) або формулою (аналітичний спосіб задавання функції).
|
ТО функція |
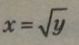 |
називається оберненою по відношенню до заданої
Буква / — це символ функції.
Табличний спосіб задавання функції полягає в тому, що в таблиці задані значення аргументу і відповідні значення функції ( для кожного значення аргументу).
Значення аргументу і значення функції записуються в різні рядки таблиці, але виключно по стовбчиках розміщується кожна пара значень аргументу і функції.
Недоліком табличного методу задавання функції є мала наочність функціональної залежності, але його перевагою служить відносно велика точність обчислень.
|
Приклад. |
 |
|
При графічному способізадавання функції в системі координат проставляється ряд точок, що відповідають значенням функції і аргументу. Потім ці точки сполучають плавною лінією. Для побудови такого графіка функції можна використати і таблицю, і формули залежності аргументу від функції. |
 |
|
Значення залежної змінної називається значенням функції. Усі значення, яких набуває аргумент, утворюють область визначення функції. |
4.2. Область визначення і область значень функції
Означення. Область визначення функції у “/(*■) — це множина
всіх значень незалежної змінної х, при яких функція визначена.
Якщо задана функція і її область визначення не вказана, то вважають, що область визначення функції — це всі значення аргументу, при яких ця функція має смисл.
Областю визначення функції може бути інтервал чисел; частина числової осі, обмежена з однієї сторони певним значенням (числом); усі значення чисел на числовій осі, крім одного або декількох заданих чи означених якимось правилом чисел.
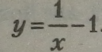
До н області визначення
Пр и к л а д и. Задана функція
не входить число 0, оскільки воно перетворює знаменник дробу на 0 і все рівняння втрачає зміст. Якщо немає інших обмежень, то областю визначення даної функції будуть усі числа осі абсцис, крім 0.
Областю визначення функції у = Xіє множина всіх дійсних чисел, тобто х є R.
Областю визначення функції у = х3 теж є множина всіх дійсних чисел, тобто

Якщо площа прямокутника із сторонами 6 іясм має область визначення від 10 см до 15 см, то другий вимір прямокутника (*) може змінюватись чисельно від 10 до 15 см, тобто 10 < х < 15.
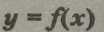 |
— це множина |
Означення. Область значень функції
всіх значень, яких набуває залежна змінна у (при х, які належать області її визначення).
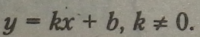
Область визначення функції є множина дійсних чисел, тобто хє R. Областю значень функції є множина дійсних чисел, тобто у є R.
Графік функції
Означення. Графік функції — це множина всіх точок на координатній площині, абсциси яких дорівнюють значенням аргументу, а ординати — відповідним значенням функції.
Графік функції залежить від виду функції (лінійна, квадратична, кубічна, обернена пропорційність і т. д.).
Графіки лінійної функції з однією змінною і функції прямої пропорційності — це завжди прямі. Для їх побудови достатньо знати координа-тт двох точок (частіше за все — точок перетину з осями координат).
Інші функції (коли аргумент представлений степенем з показником, більшим за 1, обернена пропорційність, тригонометричні і логарифмічні функції) — криві, тому їх побудова частіше за все виконується схематично (приблизно вказується напрямок віток функції, визначаються точки перетину з осями і перетин або неперетин графіком функції точки початку координат).
Для побудови графіка функції може бути задана область визначення функції або область значень функції (квадрант площини, додатна або від’ємна піввісь, графічні числові значення по осях).
Для схематичного зображення графіка функції вимагається знання його загального виду.
Приклади.
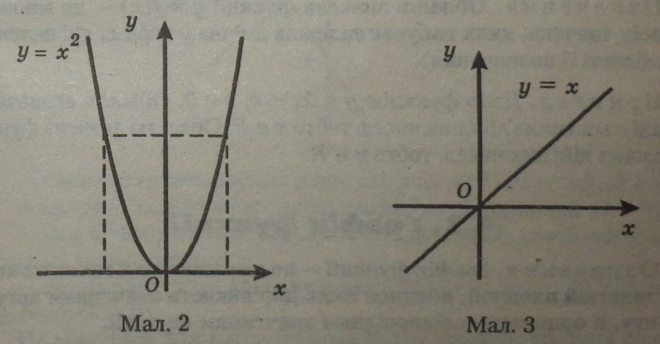
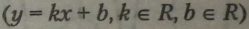 |
є пряма (мал. 4); |
|
Графіком лінійної функції |
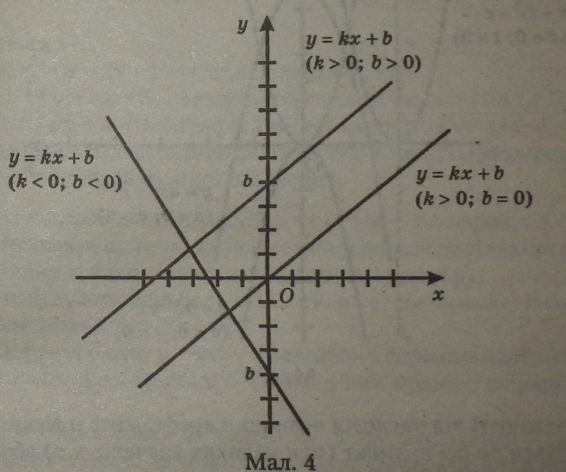 |
— пряма нахилена вправо, якщо коефіцієнт k додатний (k > 0);
— пряма нахилена вліво, якщо коефіцієнт k від’ємний (k < 0);
— чим більше числове значення коефіцієнта k, тим ближче пряма підходить до осі ординат;
— пряма перетинає додатну піввісь ординат, якщо (b > 0), і від’ємну, якщо (Jb <0).
На координатній площині подано три графіки лінійної функції. Два графіки паралельні між собою (коефіцієнти k у них однакові за знаком і чисельно) і обидва перетинаються з третім графіком, у якого коефіцієнт має протилежний (від’ємний) знак.
У двох графіків коефіцієнти при * однакові, отже, графіки паралельні, але перенесені один відносно другого на Н
У графіка, який проходить через початок координат — точку О (0; 0), вільний член відсутній (Ь * 0).
Третій графік, який перетинає паралельні графіки, має від'ємний коефіцієнт <k < 0), від’ємний вільний член (6 < 0), на його абсолютну величину графік перенесений вниз від осі х.
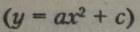
Графік квадратичної функції
— це парабола (мал. 5),
вершина якої зміщена на відстань |с| одиниць по осі ординат вгору, якщо с > 0, і вниз, якщо с < 0.
|
Вітки параболи направлені вгору (якщо а > 0) або вниз (якщо а < 0). |
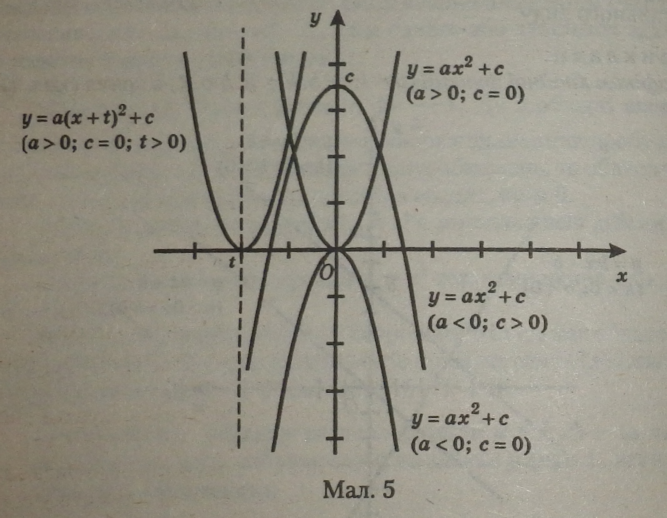 |
У залежності від числової величини коефіцієнта а вітки параболи наближаються до осі ординат (при великих значеннях а) або відхиляються від осі ординат (при малих значеннях а).
Парабола може бути несиметрична відносно осі ординат, а вісь симетрії параболи може розташовуватись по прямій, паралельній осі орди
-це
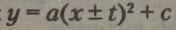 |
[вісь симетрії |
нат, у цьому випадку рівняння має вигляд:
перенесена на И одиниць по осі абсцис вліво або вправо).
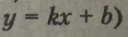
Графік лінійної функції (загальний вигляд функції
завжди пряма лінія (мал. 4), яку можна побудувати точно по двох точках (аксіома 1 геометрії).
При схематичній побудові треба знати особливості зображення графіка лінійної функції за зовнішнім виглядом рівняння.
Якщо лінійна функція має вигляд у = kx (відсутній вільний член рівняння, 1В 0), то пряма проходить через точку початку координат (0, Ц
а ДРУ1^ точку можна обчислити, взявши будь-яке дійсне значення хі
обчисливши у.
Якщо коефіцієнт при аргументі (£) додатний, то пряма проходить через І і НІ квадранти (нахилена вправо), якщо коефіцієнт від’ємний, то пряма проходить через II і IV квадранти (нахилена вліво).
Чим більше k, тим ближче до осі ординат знаходиться пряма, а чим менше — тим ближче пряма до осі абсцис.
Якщо функція має вигляд у -kx+b (є вільний член рівняння, Ь * 0), то графік функції не проходить через початок координат, а перенесений по осі ординат на \Ь\ одиниць вгору при b > 0 або на \Ь\ одиниць вниз при *<0.
Якщо у двох лінійних функцій коефіцієнти рівні, то графіки функцій паралельні. Якщо коефіцієнти не рівні, то графіки функцій перетинаються.
|
Приклади. |
 |
|
Якщо в рівнянні відсутній доданок з аргументом (рівняння виду у = Ь), то графік функції паралельний осі абсцис. |
Графік квадратичної функції у = ах2 + с — це парабола (мал. 5), яку треба будувати по точках (значення хдаються довільно; підставивши в рівняння х, обчислюємо відповідні значення у).
Щоб побудувати параболу схематично, треба проаналізувати рівняння таким чином.
Графік функції виду у = ах2 — це парабола, вершина якої розташована в точці початку координат О (0; 0), а вісь ординат служить віссю симетрії.
При а > 0 вітки параболи напрямлені вгору, а при а < 0 — вниз. Чим більше значення а, тим ближче до осі ординат розташовані вітки параболи, а чим менше а, тим далі.
Якщо рівняння має вигляд у — а(х+ £)2, то парабола виду у ** ах1 перенесена вліво на величину \t\ по осі абсцис при t > 0, і вправо на величину |і| по осі абсцис при t<0.У відповідній точці (t,0) на осі абсцис треба провести пряму, паралельну осі ординат, яка і буде віссю симетрії для графіка такого виду.
Графік функції у - ах1+ с або у •= а(х+ t)2 + с — це парабола, як у графіка функції вигляду у = ах? (у ~ а (х + ї)2)> але перенесена по осі ординат на |с| одиниць вгору при с > 0 або на |с| одиниць вниз по осі ординат при с < 0.
Обернено пропорційною називається функція виду
є множина всіх дійсних чисел,
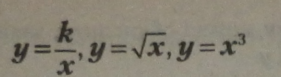
4.4. Функції
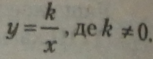
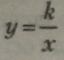
Областю визначення функції
|
крім 0. Графіком оберненої пропорційності є крива, яка називається гіперболою (мал. 6). Гіпербола — це крива, що має дві вітки, симетрично розміщені відносно точки початку координат О (0; 0). Вітки параболи при k > 0 розміщені в І і II квадранті, а при k < 0 — в II і IV квадрантах. |
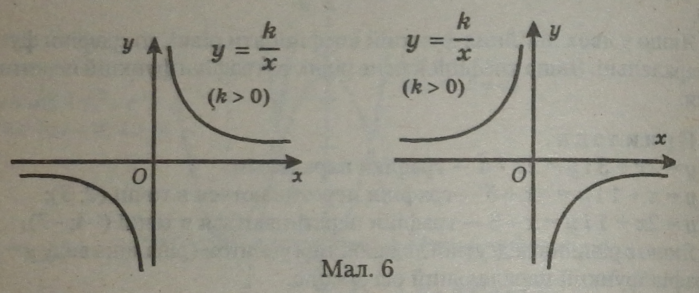 |
Оскільки точка початку координат не входить в область визначення функції, то гіпербола не перетинає осей координат. Вітки гіперболи наближаються до осей, але не досягають їх навіть при нескінченно великих (малих) значеннях х. Говорять, що графік функції переривається в точці початку координат, а вітки параболи в точках, близьких до початку координат, ідуть у нескінченність.
Для побудови гіперболи необхідно створити таблицю значень у при довільно взятих числових значеннях х. Одержані точки сполучити плавною кривою лінією.
|
Функція |
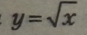 |
завжди додатна. |
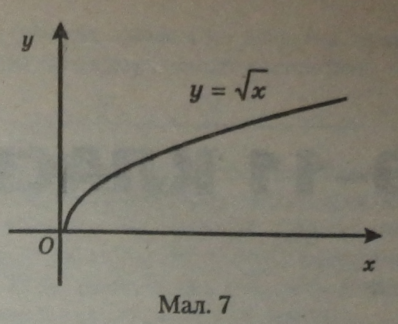
Областю визначення функції є множина невід’ємних дійсних чисел. Графіком функції служить одна вітка параболи, розміщена в І квадранті, оскільки аргумент і функція одночасно додатні тільки в цьому квадранті (мал. 7).
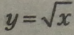
, треба скласти таблицю значень функції для деяких значень аргументу х. Відмітивши точки, координати яких подані в таблиці, сполучити їх плавною лінією.
Обчислення значень у частіше за все наближені (з округленням результату).
Чим більше числове значення аргументу (х), тим більше числове значення функції (у), тобто функція
Щоб побудувати графік функції
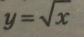
зростає на всій області ви
значення.
Функція у* х3 — up степенева функція, якій відповідає графік, що називають кубічною параболою.
Фізичний зміст функції — це залежність об’єму куба (у) від його ребра (х).
Будується кубічна парабола по точках за допомогою таблиці, в якій довільно заданому значенню аргументу х відповідає визначене значення функції (у).
Кубічна парабола має дві вітки (мал. 8), одна розміщена в І квадранті (при додатному х додатний і у), а друга в III квадранті (при від’ємно* мул: від’ємний і у). Вітки параболи напрямлені вгору і вниз, тому що для будь-якого додатного і від’ємного числа існує куб цього числа. Точкою симетрії графіка кубічної параболи є точка початку координат О (0; 0), через яКу проходить парабола.
Властивості графіка функції у-&
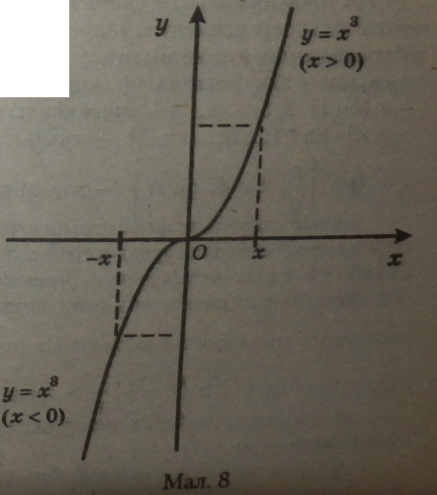
1. Область визначення функції — вся числова пряма.
2. Якщо х * 0,то і у - 0. Парабола проходить через точку початку координат О (0; 0).
3. Якщо х > 0, то і у > 0. Куб додатного числа, відмінного від 0, є число додатне, тому в параболи одна вітка розміщена в додатному квадранті. Якщо х<0,тоіу<0,оскільки непарний степінь від’ємного числа
— число від’ємне; друга вітка параболи розміщена у від’ємному квадранті.
Автор: admin от 8-06-2013, 22:42, Переглядів: 49011