Суміжні й вертикальні кути, паралельні й перпендикулярні прямі
Суміжні й вертикальні кути
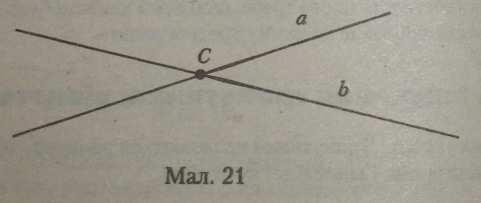
Якщо прямі а і В перетинаються в точці С, то С є а і С е Ь, і немає ніякої іншої точки, крім С, яка належала б обом прямим одночасно.
Дві прямі, що перетинаються, у точці перетину (мал. 21), як при вершині (Q, утворюють 4 кути, сторонами яких служать півпрямі прямих (а і Ь), що перетинаються.
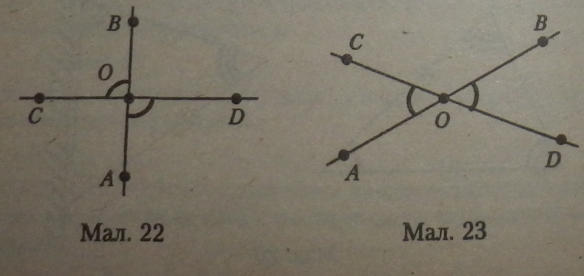
Розглянемо ці кути. Прямі АВ і CD перетинаються в точці 0, утворюючи пару гострих кутів (ZC0A і ZB0D) і пару тупих кутів {/.СОВ і ZAOD) (мал. 23). Кути кожної пари називаються вертикальними. Вертикальні кути рівні між собою.
Означення. Вертикальні кути — це пара кутів, що мають спільну
Вершину, а сторони одного кута є доповняльними шапрямимн сторін другого кута.
На мал. 23 /СОА “ Z. BOD і /СОВ “ ZAOD, оскільки в них спільна вершина О; а ОВ і СО, АО і 0D — доповняльні півпрямі прямих АВ і CD.
У будь-яких двох прямих, що перетинаються, утворюється по дві пари вертикальних кутів, які можуть бути:
— парою тупих кутів і парою гострих кутів (мал. 23);
— прямими кутами (мал. 22).
Розглянемо ще раз мал. 22 і 23.
За аксіомою 5 сума кутів {/.СОВ і ZBOD; /BOD і /АОЕУ, ZAOD і /СОА /СОА і /.СОВ) дорівнює розгорнутому куту (ZAOB або /.COD), тобто 180е. Пари таких кутів є суміжними кутами.
При перетині двох прямих утворюється 4 пари суміжних кутів:
/СОВ I /BOD і 180е; /BOD | /AOD Щ180*;
ZAOD + /СОА -180е; /СОА + /СОВ « 180е.
Означення. Суміжні кути — це пара кутів, в яких одна сгорова
Спільна, а дві інші є доповняльними нівпрямими.
Суміжні кути утворюються тоді, коли з вершин розгорнутого кута до однієї півплощі проведено промінь.
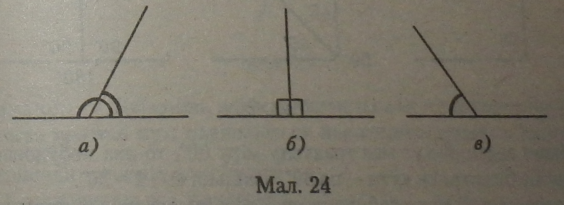
У пари суміжних кутів кути бувають:
— гострий і тупий (мал. 24, а і'24, в);
— прямі (мал. 24, б).
Означення. Бісектрисою кута називається промінь, який виходить із вершини кута, проходить між його сторонами і ділить кут пополам. Бісектрису кута можна побудувати за градусною мірою кута за допомогою транспортира. Для цього градусну міру заданого кута ділять
Пополам і на одній із сторін від вершини відкладають градусну міру половинного кута. Друга сторона такого кута буде бісектрисою заданого кута.
Щоб побудувати бісектрису кута, не обчислюючи його градусну міру, треба використати циркуль (див. мал. 25):
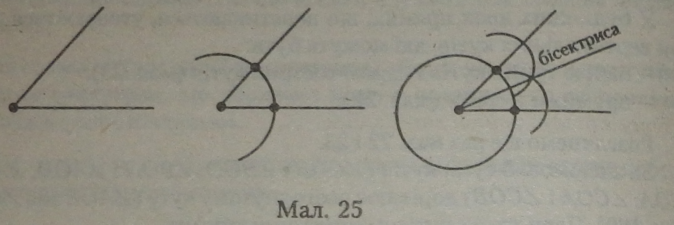
1.3 вершини кута будь-яким радіусом провести дугу кола, щоб вона перетнула сторони кута.
2.3 кожної точки перетину дуги і сторін кута іншим радіусом провести дуги кіл. Точка перетину дуг у площині кута належить бісектрисі кута.
3. Сполучимо одержану точку і вершину заданого кута променем, який і буде бісектрисою Заданого кута.
Прямий і розгорнутий кути з бісектрисою показані на мал. 26.
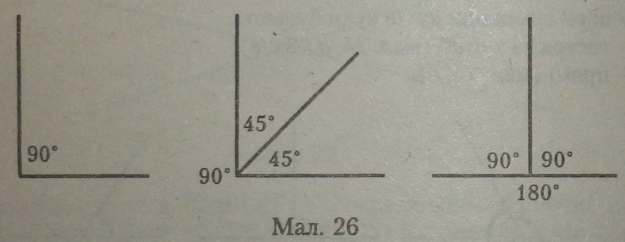
Якщо заданий кут має градусну міру 60е, то два побудованих за допомогою бісектриси кути — по 30е, оскільки 60°: 2 = 30°.
Розгорнутий кут розбивається бісектрисою на два прямих кути (180°: 2 = 90°), будь-який тупий кут розбивається бісектрисою на два гострих кути.
Паралельні й перпендикулярні прямі
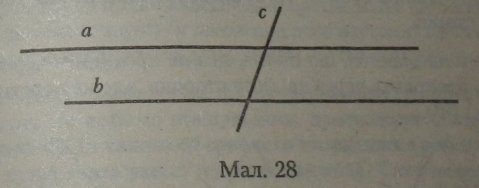
Означення. Дві прямі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.
А „„ w н^,,аралып-"» прямій ь, оскільки вони не перегнуться, скільки 6 ми IX не продовжувала Для позначення паралельності використовується знак ||. Запис а||6 читається як «пряма а паралельна прямій Я
Основна властивість паралельних прямих: якщо дві прямі (а і с) паралельні третій прямій (Ь), то вони паралельні між собою (а|с).
Якщо ми візьмемо точку А і пряму с, то через точку А можна провести нескінченну множину прямих, але тільки одна з них буде паралельна с.
Аксіома 9 (властивість паралельних прямих). Через точку, що не лежить на даній прямій, можна провести на площині не більше як одну пряму, паралельну даній.
 |
|
Якщо пряма (с) перетинає одну з паралельних прямих (а), то вона повинна перетнути і другу паралельну пряму (Ь). |
Означення. Дві прямі, які перетинаються і в точці перетину утворюють прямий кут, називаються перпендикулярними прямими.
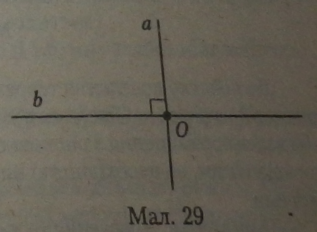
Перпендикулярні прямі (вертикальна і горизонтальна) утворюють осі координат на площині. У точці перетину перпендикулярних прямих усі кути прямі. Перпендикулярність прямих можна позначити знаком перпендикулярності JL. Так, запис: a Lb питається як «пряма а перпендикулярна до прямої Ьь.
Через кожну точку прямої можна провести до цієї прямої перпендикулярну пряму.
Означення. Перпендикуляром до даної прямої називається від. різок прямої, перпендикулярної до даної прямої, який мас од. ним Із своїх кінців їхню точку перетину. Цей кінець відрізка Що зивається основою перпендикуляра.
Через дану точку прямої можна провести тільки один перпендикуляр, решта прямих, які перетинаються з даною прямою, будуть похилими до цієї прямої.
Аксіома — це твердження, яке приймають без доведення.
Теорема — це твердження, яке доводять. При доведенні використовуються як аксіоми, так і раніше доведені теореми.
Формулювання теореми містить умову (це те, що дано) і висновок (те, що доводиться в теоремі).
Означення. Теорема — це твердження, у правильності якого впевнюються за допомогою доведення.
Сформулюємо першу теорему.
Теорема 1 (про перетин сторін трикутника прямою). Якщо пряма, яка не проходить через жодну з вершин трикутника, перетинає одну з його сторін, то вона перетинає тільки одну з двох інших сторін.
Ми повинні довести, що пряма, яка не проходить через вершину трикутника, проходить через дві його сторони, але не перетинає третю сторону (мал. ЗО).
До початку доведення теореми нам треба зробити малюнки геометричних фігур, про які йде мова в умові теореми, пов’язавши їх розміщення або взаєморозміщення з висновком теореми. Малюнок може бути бата* товаріантним, за необхідністю виконують декілька малюнків до одні# теореми.
Доведення. Доведення теореми основане на аксіомі 4 (властивій розміщення точок відносно прямої на площині).
Пряма (а) розбиває площу трикутника на дві півплощини, |Ш| якщо вона не проходить через вершину трикутника, то одна з вершин знаходиться в одній ггівплощині, а дві інші — в другій півплощині.
Сторона трикутника, яка сполучає дві вершини водній пі «площині, не може перетинати пряму в площині трикутника. Такий перетин можливий за таких умов:
1) сторону трикутника продовжити і продовжити пряму, тоді перетин можливий за площинок) трикутника;
2) якщо пряма не паралельна третій стороні (при паралельності прямої одній із сторін, вона за означенням паралельних прямих не може перетнутися з третьою стороною трикутника).
Обидві ці умови не відповідають умові теореми, оскільки пряма за умовою розглядається лише в площині трикутника (нас цікавлять сторони трикутника, які обмежують цю площину, отже, належать площині трикутника).
Теорема доведена.
Висновки теореми
1. Будь-яка пряма, яка проходить через площину трикутника, але не через його вершину, перетинає тільки дві сторони цього трикутника.
2. Відрізки, розміщені в одній півплощині, не перетинають пряму, що ділить площину на дві ггївплощини.
Ці висновки можна використати при доведенні інших теорем і при розв’язуванні задач.
Ми розглянули пряме доведення теореми. Існує ще спосіб доведення теоремі що застосовується також при розв’язуванні задач на доведення, такий спосіб називається доведенням від супротивного.
Означення. Доведення від супротивного полягає в тому, що спочатку ми робимо припущення, протилежне висновку теореми (задачі). Із такого оберненого твердження робимо висновок, який суперечить умові теореми (задачі). Таке доведення відкидається, а висновок теореми (пряме твердження) пргёмастъся як правильний.
Отже, якщо доведення від супротивного правильне, то теорема в частині висновку неправильна (не доводиться).
Розглядаючи суміжні кути у розділі 1.6, ми ознайомилися з теоремою 2.
Теорема 2 (про суміжні кути). Сума суміжних кутів дорівнює 180е.
Д о в е д е н н я. Доведення цієї теореми зводиться до аксіоми 5 (властивість вимірювання кутів). На основі цієї аксіоми ми стверджуємо, що Розгорнутий кут має градусну міру 180
Наступним твердженням цієї аксіоми служить визначення градусної міри кута, як суми градусних мір кутів, на які він розбивається.
Доведення теореми основане на побудові (використовується визначення суміжних кутів). Суміжні кути утворюються тоді, коли між сторонами розгорнутого кута проходить промінь з його вершини.
Висновки теореми
1. Якщо два кути рівні, то суміжні з ними кути також рівні.
2. Якщо кут не розгорнутий, то його градусна міра менша від 180е.
3. Кут, суміжний з прямим кутом, також прямий.
Теорема 3 (про рівність вертикальних кутів). Вертикальні кути рівні.
Доведення. Ця теорема доводиться на основі теореми 2 і ї| висновків.
При перетині двох прямих розглядають пари суміжних кутів при кожній з прямих (пряма служить сторонами розгорнутого кута). Якщо у двох пар суміжних кутів є по одному рівному куту, то й другі кути теж рівні. Для доведення з кожної пари береться один кут, спільний і для однієї пари суміжних кутів, і для другої (мал. 23, розділ 1.6).
Теорема 4 (про перпендикуляр з точки на прямій). Через кожну точку прямої можна провести перпендикулярну до неї пряму, і тільки одну.
Доведення. Теорема доводиться методом від супротивного. Припустимо, що з однієї точки до прямої проведено два перпендикуляри, що не суміщаються. 1
За означенням перпендикулярних прямих кут між перпендикуляром і прямою дорівнює 90°, отже, і суміжний з ним кут теж 90е (за теоремою 2).
Виходить, ми зробили неправильне припущення, оскільки два перпендикуляри повинні мати однаковий кут нахилу до прямої (90°), тобто суміститись. Оскільки такого не трапилося і в точці з прямою перетинаються дві видимі прямі, то кут нахилу в другої прямої, щоб вона була видимою, повинен бути меншим за 90°, тобто друга пряма — похила, а не перпендикуляр. Наше припущення помилкове, а висновок теореми правильний.
Автор: admin от 10-06-2013, 17:30, Переглядів: 25109