Декартова система координат на площині

Прямокутна система координат на площині

Означення. Дві взаємно перпендикулярні прямі утворюють прямокутну систему координат. Прямі х і у називаються осями координат. Пряма х — вісь абсцис, а пряма у — вісь ординат. Точка перетину прямих (точка О) називається початком коор-динаТо На кожній з осей вибирається довільний масштаб (адини* чний відрізок).

Кожній точці площини, наприклад А, відповідає одна пара чисел (*; у), що називається координатами точки на площині. Пишуть А (х; у).

Вісь абсцис (вісь х) точкою О (0; 0) ділиться на дві півосі: праворуч від точки О — додатна піввісь, а ліворуч — від’ємна піввісь.

Вісь ординат (вісь у) точкою О теж ділиться на дві півосі: угору від точки О — додатна піввісь, а вниз — від’ємна піввісь (мал. ЗО).

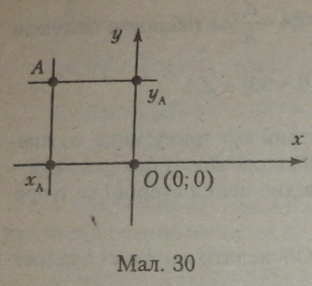
Якщо задано точку на площині pH го її координати визначаються і записуються в такий спосіб:

1.  З точки А опустити перпендикуляр на вісь х. Числове значення (кількість одиничних відрізків від початку координат до основи перпендикуляра) точки на осі х—хА — є першою координатою точки А.

2.  На вісь у опустити перпендикуляр із точки А. Числове значення (кількість одиничних відрізків від початку координат до основи перпендикуляра) точки на осі у—уА — є другою координатою точки А.

3.  Записати отримані координати точки в круглих дужках у такий спосіб: А (хА; ул). Значення хА і ук записуются зі. своїми знаками.

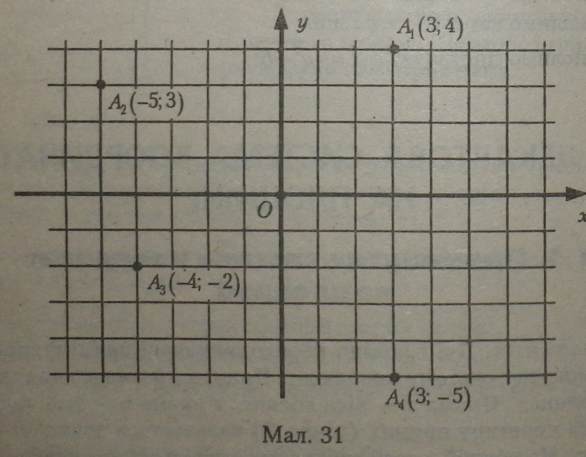
Координатна площина осями абсцис і ординат поділяється на 4 чверті, або квадранти. Точка Ах розташована в І квадранті, точка А — у II квадранті, точка А3 — у III квадранті, точка Л4 — у IV квадранті (мал. 31).

Означення. Декартові координати на площині — це проекції точки на цій площині на осі декартових координат.

Характеристика квадрантів площини декартової системи координат:

I  квадрант — це площина, обмежена додатними півосями абсцис І ординат. Обидві координати будь-якої точки площини мають знак «+».

II  квадрант — це площина, обмежена від’ємною піввіссю абсцис і додатною піввіссю ординат. Абсциса будь-якої точки площини має знак «-», а ордината — знак «+>.

III  квадрант — це площина, обмежена від'ємними півосями абсцис

І ординат. Обидві координати будь-якої точки площини мають знак *->.

IV  квадрант — це площина, обмежена додатною піввіссю абсцис і від’ємною піввіссю ординат. Абсциса будь-якої точки площини має знак

А ордината — знак «М.

Точки, розміщені на утворюючих осях, мають завжди одну координату, що чисельно дорівнює 0. Точки осі абсцис мають координату 0 на осі ординат, а точки осі ординат мають координату 0 на осі абсцис. Точка, що потрапляє на початок координат, має координати (0; 0).

Перпендикуляри з точки на осі і відрізки на осях (мал. 32) утворюють прямокутник, одна вершина якого належить точці (В) площини, дві лежать на осях (Я, і В2) і четверта збігається з точкою початку координат (О). Точки, що належать осям (В, і В2), і дадуть координати заданої точки В.

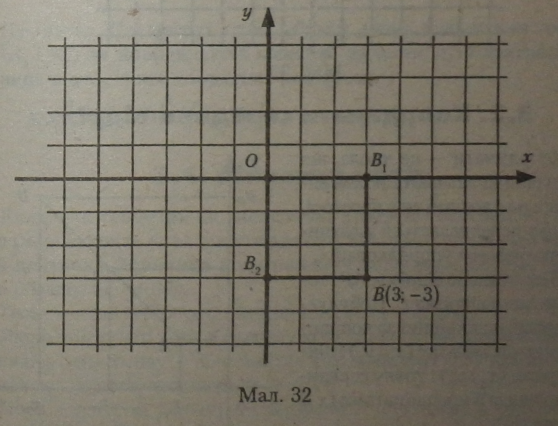
Довжина відрізків ОВх і ОВ2 — це числове значення координат точки, воно дорівнює відстані від проекції точки на вісь до точки початку координат.

Будь-яку геометричну фігуру на площині можна побудувати заточками, але ми використовуємо аксіому 1 (через дві точки можна провестя пряму і тільки одну), чим значно скорочується процес побудови.

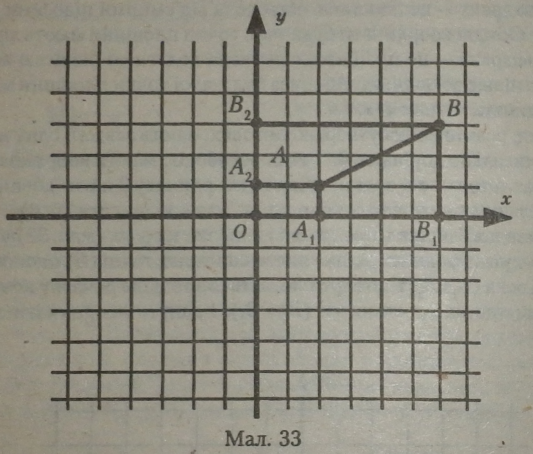
Відрізок прямої, що сполучає дві будь-які точки на площині (мал. 33), теж має проекції на утворюючі осі, величина яких дорівнює різниці довжин сторін допоміжних прямокутників ОА{АА2, ОВхВВг

Відрізок прямої (АВ) має точки початку відрізка (А) і кінця відрізка (В) зі своїми координатами і проекції на утворюючі осі (АХВХ і