Планіметрія. Подібність фігур

ПЛАНІМЕТРІЯ

Планіметрія вивчає властивості таких плоских геометричних фігур як точка і пряма, кут, паралельні прямі, многокутники та коло. Властивості цих геометричних фігур вивчалися в курсі цього предмету раніше.

Подібність фігур

Дві фігури на площині називаються подібними, якщо в них відповідні кути рівні, а відповідні відрізки — пропорційні. Наприклад, у подібних

Ознаки подібності трикутників

Ознака подібності за двома кутами

Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого трикутника, то такі трикутники подібні.

Ознака подібності за двома сторонами і кутом між ними

Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника, і кути, утворені такими сторонами, рівні, то трикутники подібні.

Ознака подібності за трьома сторонами

Якщо три сторони одного трикутника пропорційні сторонам іншого трикутника, то такі трикутники подібні.

Подібність прямокутних трикутників

Оскільки у прямокутного трикутника один кут прямий, для P°$L НОСТІ ДВОХ прямокутних трикутників достатньо, щоб у НИХ було ПО рів му гострому куту.

А) Катет прямокутного трикутника є середне пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу.

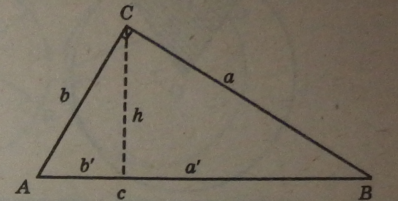
Наслідки подібності прямокутних трикутників

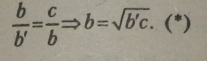
Висота прямокутного трикутника, проведена з вершини прямого кута на гіпотенузу, є середнє пропорційне між проекціями катетів на гіпотенузу.

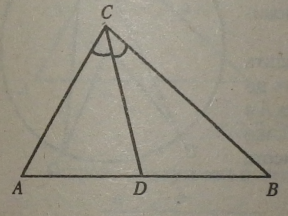
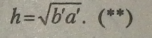
Б) Властивість бісектриси внутрішнього кута трикутника;

Бісектриса внутрішнього кута трикутника ABC ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам, тобто

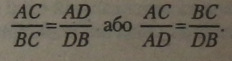
1.1.2. Теорема Фалеса

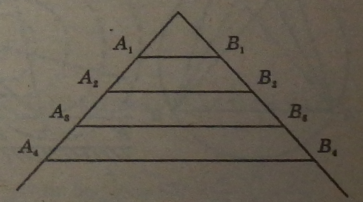
Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні.

Ця теорема застосовується Для ділення відрізка на рівні частини.

1.2. Кути, вписані в коли

1.2.1. Центральний кут

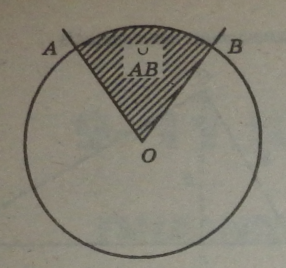
Центральним кутом (на мал. ZAOB) у колі називається плоский Ут із вершиною у його центрі. Вимірюється дугою, на яку він вимірюється у градусах або частіше в радіанах.

Градусною мірою дуги кола називається градусна міра відповідного центрального кута.

Кут, вписаний у коло

Кут, вершина якого лежить на колі, а сторони перетинають це коло, називається вписаним у коло (ZCAD).

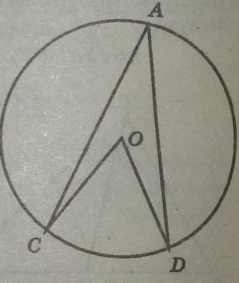
Кут, вписаний у коло, дорівнює половині відповідного центрального кута.

Вписані кути, сторони яких проходять через точки А і В кола, а вершини лежать по один бік від прямої АВ} рівні. Тому точка А є точкою найкращого огляду картини ВС, що підвішена на вертикальній стіні (А — висота від підлоги до рівня ока спостерігача).

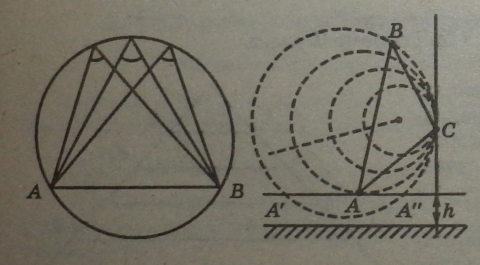
Якщо спостерігач знаходиться в точці А' або А", то треба через хорду ВС проводити кола більшого радіуса, щоб вони перетинали лінію ока, отже, кути зору ZBA'С або ZBA"C6ywn меншими, ніж /.ВАС.

Пропорційність відрізків хорд, січних і дотичної до кола

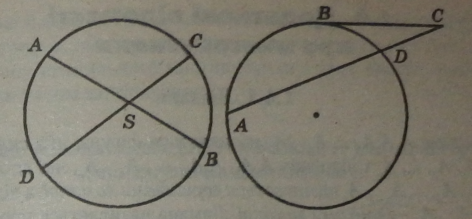
Якщо хорди АВ і CD кола перетинаються у точці S, то AS‘BS-CSDS.

Якщо із точки С, що лежить поза колом, провести дотичну В січну АС, то квадрат довжини дотичної В С дорівнює добутку довжи січної А С на її зовнішню частину, тобто #C2-ACDC.

Розв'язування трикутників

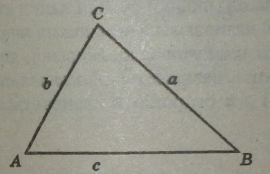
Теорема косинусів

Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.

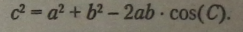
Теорема синусів

Сторони трикутника пропорційні до синусів протилежних кутів.

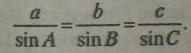
Зауваження. Якщо R — радіус описаного навколо трикутника ABC кола, то

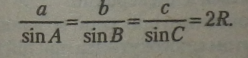
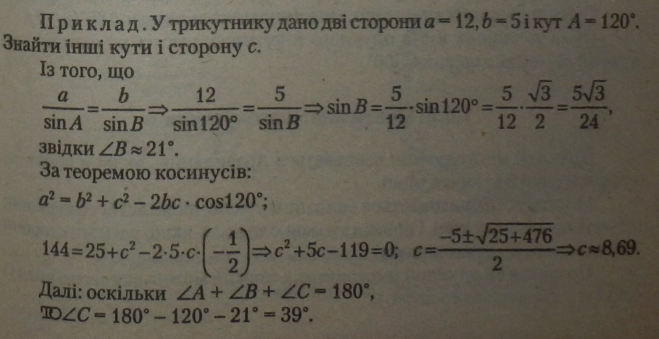
1.4.1. Ламана

Вона не має самоперетинів. Довжиною ламаної називається сума довжин її ланок.

Додаткові відомості про многокутники

Ламана називається замкненою, якщо її кінці збігаються. Проста замкнена ламана називається многокутником, якщо її сусідні ланки не лежать на одній прямій. Вершини ламаної називаються вершинами многокутника, а ланки ламаної — сторонами многокутника. Відрізки, які сполучають несувідні вершини многокутника, називаються діагоналями. Многокутник з п вершинами, а отже, і з п сторонами називається п-кутником.

Плоский многокутник

Плоским многокутником або многокутною областю називається скінченна частина площини, обмежена многокутником.

Многокутник називається опуклим, якщо він лежить в одній пів-площині відносно будь-якої прямої, яка містить його сторону. При цьому сама пряма вважається такою, що належить півплощині.

Кутом опуклого многокутника при даній вершині називається кут, утворений його сторонами, які сходяться в цій вершині.

Зовнішнім кутом опуклого многокутника при даній вершині називається кут, суміжний із внутрішнім кутом многокутника при цій вершині.

Сума внутрішніх кутів опуклого «-кутника дорівнює 180°(я - 2).

Сума зовнішніх кутів опуклого я-кутника, узятих по одному при кожній вершині, дорівнює 360е.

Правильні многокутники

Опуклий многокутник називається правильним, якщо в нього всі сторони рівні й усі кути рівні.

Многокутник називається вписаним у коло, якщо всі його вершини лежать на деякому колі, і описаним навколо кола, якщо усі його сторони дотикаються до деякого кола.  ,,

Правильний опуклий многокутник завжди можна вписати в коло І описати коло навколо нього).

Вписане й описане кола правильного многокутника мають один і самий центр, який називається центром многокутника. Кут, під яким видно сторону правильного многокутника з його центра, називається центральним кутом многокутника.  .  •<

Радіуси описаного (R) і вписаного (r) кіл правильного многокутника зі стороною а

Для правильного (рівностороннього) трикутника:

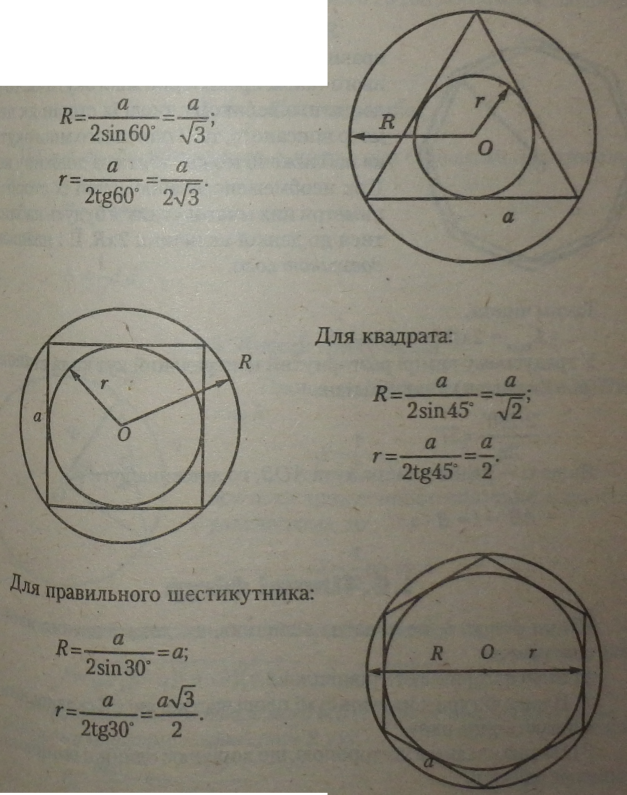Подібність правильних опуклих многокутників

Правильні опуклі n-кутники подібні. Зокрема, якщо у них сторони, то вони рівні.

Коефіцієнт подібності подібних фігур дорівнює відношенню відповідних лінійних розмірів. У правильних я-кутниках такими лінійними розмірами є довжини сторін, радіуси вписаних і описаних кіл.

У правильних л-кутників відношення периметрів, радіусів вписаних і радіусів описаних кіл рівні.

Довжина кола

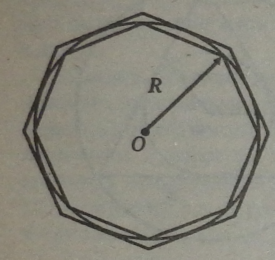
Якщо у коло даного радіуса R вписати правильний многокутник і описати навколо нього також правильний многокутник, то при достатньо великому числі їх сторін як периметр вписаного, так і описаного многокутника наближено можна взяти за довжину кола. При необмеженому збільшенні їх сторін периметри цих многокутників будуть наближатися до деякої величини 2nR. Її і називають довжиною кола.

Площі фігур

Площа фігури — це додатна величина, числове значення якої має такі властивості:

1)  Рівні фігури мають рівні площі.

2)  Площа фігури дорівнює сумі площ частин, які є її складовими і не перекривають одна одну.

3)  Площа квадрата зі стороною, що дорівнює одиниці вимірювання, дорівнює одиниці.

Площа квадрата

Площа квадрата зі стороною а:

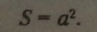
Площа прямокутника

Площа прямокутника зі сторонами а і Ь:

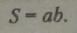
Площа паралелограма

Площа паралелограма зі сторонами а і b або з основою а і висотою h:

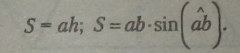
Площа ромба

Площа ромба зі стороною а, кутом між сторонами а, діагоналями d₁ і d₂

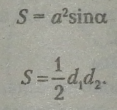
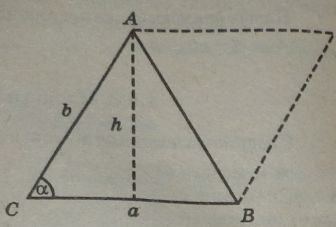
Площа трикутника

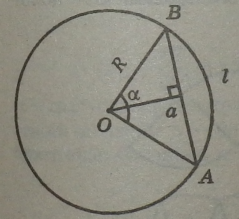
Площа трикутника з основою а і висотою h:

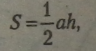
Оскільки трикутник становить половину паралелограма, то

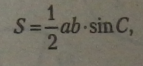
Або, виходячи з відомих сторін трикутника а, b і с,

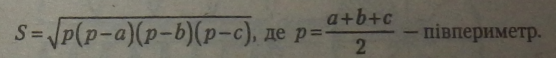Співвідношення між сторонами а, Ьіс трикутника, який має площу S, і радіусами вписаного гі описаного R кіл:

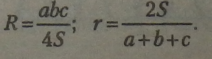
Співвідношення у правильному трикутнику зі стороною а (г— радіус вписаного кола, R — радіус описаного кола):

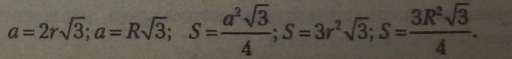Площа круга

Площа трапеції з основами а, b і висотою h:

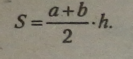Площа трапеції

Кругом називається фігура, яка складається з усіх точок площини, відстань від яких до даної її точки О, що називається центром, не більша від даного числа R, яке називається радіусом круга.

Межею круга є коло з тим же центром і радіусом.

Площа круга дорівнює половині добутку довжини кола, що його обмежує, на радіус. Це видно з малюнків а, б, в, де, послідовно розрізаючи круг на сектори (4, 8, 16,32...) і послідовно їх складаючи, бачимо, що |||§1 наближається до площі прямокутника зі сторонами nR — половина довжини кола і R.

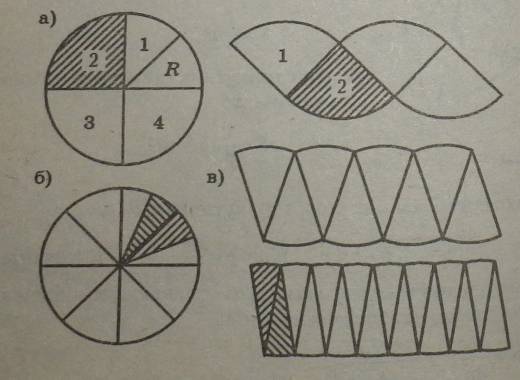
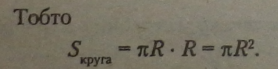
Круговим сектором називається частина круга, яка лежит у ^ ні відповідного центрального кута.