Чотирикутник, Елементи чотирикутника, паралелограм, прямокутник, ромб, квадрат
Елементи чотирикутника
Означення. Чотирикутник — це плоска геометрична фігура, що складається з чотирьох точок (вершин) і чотирьох відрізків, які послідовно сполучають їх (сторін).
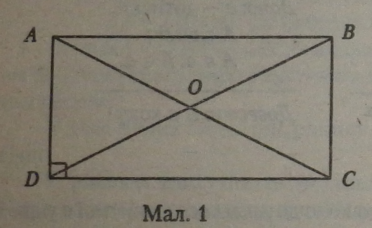
Чотирикутник назйвається за точками його вершин, ABCD (мал. 1).
Можна сказати, що чотирикутник — це замкнута ламана з чотирьох ланок. Вершини чотирикутника називаються сусідніми, якщо вони є точками, що належать одній стороні чотирикутника (А і В, В і С, С і D, D і А). Вершини чотирикутника як точки позначаються великими латинськими буквами (А, В, Сі D). Сторони чотирикутника називаються за буквами двох сусідніх вершин, які належать стороні (АВ, ВС, CD, AD).
Несусідні вершини чотирикутника називаються протилежними (А і С, В і D). Відрізки, що сполучають протилежні вершини чотирикутника, називаються його діагоналями (АС і BD). У чотирикутника дві діагоналі, і вони завжди перетинаються в одній точці (О).
Дві сусідні сторони мають одну спільну вершину (АВ і ВС, ВС і CD, CD і AD, AD і АВ). Сторони, що не мають спільної вершини, називаються протилежними (AD і ВС, АВ і CD).
Сума довжин сторін чотирикутника — це його периметр.
Периметр чотирикутника записується так:
Pabcd ~AB + BC+CD + AD.
Перпендикуляр, опущений з вершини чотирикутника на основу» називається висотою. У прямокутного чотирикутника висотою буде одна зі сторін, яка утворює з основою прямий кут (висота AD до основи DQ-
Паралелограм
Означення. Паралелограм — це чотирикутнику у якого протилежні сторони паралельні.
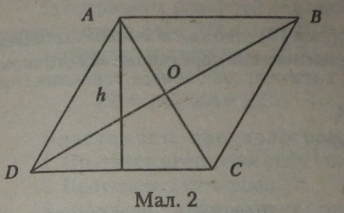
У паралелограма протилежні кути рівні. Сума всіх внутрішніх кутів паралелограма дорівнює 360*.
Паралелограм — найбільш важливий з чотирикутників. Його властивості наведені у теоремах 19,20,21.
Теорема 19 (про визначення паралелограма за його діагоналями). Якщо діагоналі чотирикутника перетинаються і точкою перетину діляться пополам, то такий чотирикутник — паралелограм.
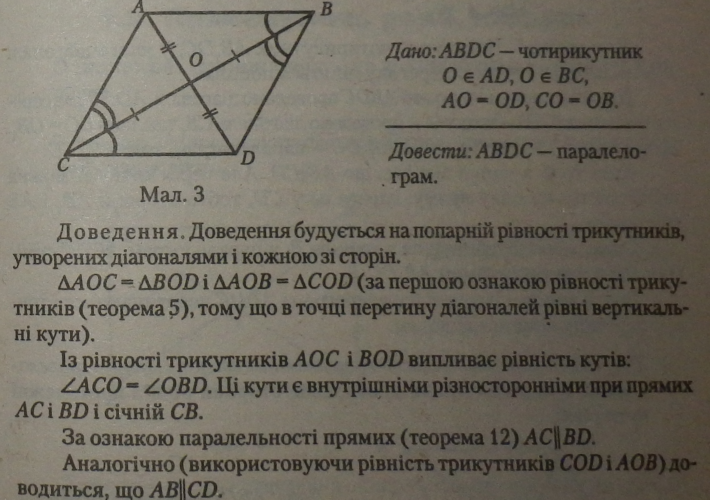
За означенням (чотирикутник, у якого протилежні сторони паралельні — паралелограм) чотирикутник ABDC є паралелограмом, що й потрібно було довести.
Теорема 20 — це теорема, обернена до теореми 19. Обернені теорема в умові використовують твердження прямої теореми, а у тверд женні теореми ставиться умова прямої теореми.
Обернена теорема 20 в умові вказує на паралелограм, а в прямій теоремі 19 доводиться, що чотирикутник — паралелограм. У прямій теоремі в умові діагоналі перетинаються і точкою перетину діляться пополам, а в оберненій теоремі потрібно довести, що діагоналі точкою перетину діляться пополам.
Т е орем а 20 (обернена до теореми 19) (про властивості діагоналей паралелограма). Діагоналі паралелограма перетинаються і точкою перетину діляться пополам.
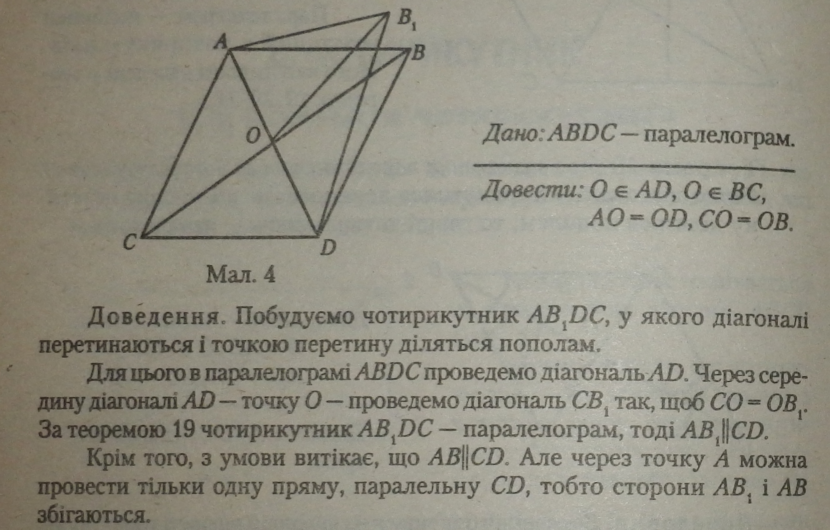
Отже, точка Вх збігається з точкою В, а паралелограм ABDC суміщається з паралелограмом ABfiC.
Таким чином, діагоналі паралелограма ABDC перетинаються і точкою перетину діляться пополам.
Теорема 2 і (про властивості протилежних сторін і кутів паралелограма). У паралелограма протилежні сторони рівні і протилежні кути рівні.
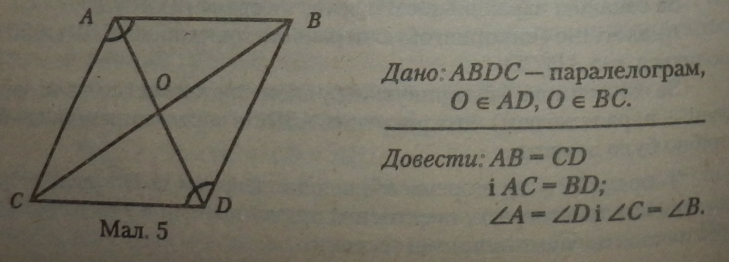
Доведення. Використовуючи теорему 20 (ДО - ОД СО - ОВ) і рівність вертикальних кутів при вершині О, за першою ознакою рівності трикутників одержуємо:
ДДОС-ДВОД АЛОВ - ACOD.
Із одержаних рівностей випливають рівності протилежних сторін паралелограма АС - BD; АВ - CD.
Із рівності трикутників i4BD і ACD, САВ і BDC (за трьома сторонами) випливає, відповідно, рівність кутів:
ZB - ZC; ZA - ZD.
Властивості паралелограма
1. Протилежні сторони рівні і паралельні між собою.
2. Протилежні кути рівні.
3. Діагоналі перетинаються і точкою перетину діляться пополам.
4. Кожна діагональ ділить паралелограм на два рівні трикутники.
5. Діагоналі в точці перетину, як вершині, утворюють 4 трикутники, які попарно рівні і мають в основі паралельні прямі.
Прямокутник, ромб, квадрат
Означення. Прямокутник — це паралелограм, у якого всі кутя
Прямі.
Теорема 22 (прорівність діагоналей прямокутника) Діагоналі пря~
Мокутника рівні. v -М
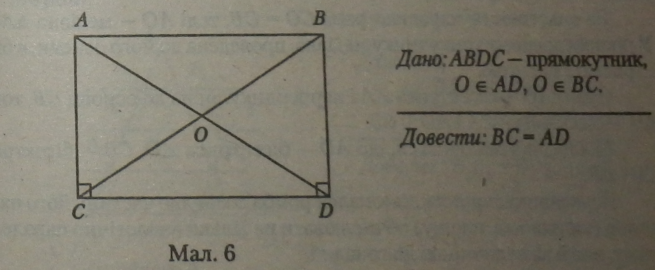
Доведення. Для доведення використовуємо той факт, що AACD-ДВCD за першою ознакою рівності трикутників (CD — спільна, АС - BD як протилежні сторони паралелограма, ZC-ZD - 90*). А в рівних трикутниках проти рівних кутів (у цьому випадку прямих кутів) лежать рівні сторони.
Отже, ВС - AD, як гіпотенузи рівних прямокутних трикутників, ще й необхідно було довести.
Властивості прямокутника
1. Протилежні сторони рівні й паралельні.
2. Усі кути прямі.
3. Діагоналі рівні, перетинаються в одній точці і точкою перетину діляться пополам.
4. Кожна діагональ ділить прямокутник на два рівні трикутники.
5. Точка перетину діагоналей є спільною вершиною чотирьох трикутників, які попарно рівні і мають в основах паралельні прямі.
Означення. Ромб — це паралелограм, в якого всі сторони рівні.
Теорема 23 (про діагоналіромба). Діагоналі ромба перетинаються під прямим кутом і є бісектрисами його кутів.
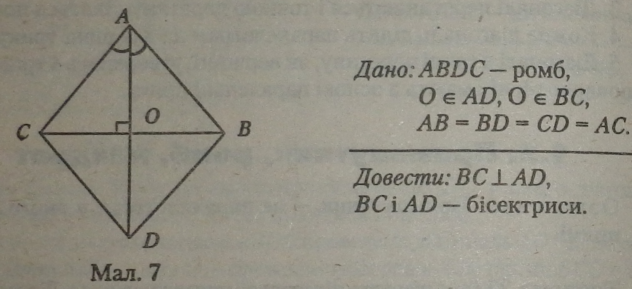

Перпендикулярність діагоналей ромба дозволяє частину його параметрів (наприклад, площу) обчислювати не тільки аналогічно паралелограму, але й за величиною діагоналей.
Властивості ромба
1. Усі сторони рівні і протилежні сторони попарно паралельні.
3. Діагоналі — бісектриси кутів, взаємно перпендикулярні, перетинаються і точкою перетину діляться пополам.
4. Діагоналі ділять ромб на дві пари рівних трикутників зі спільноіо вершиною в точці перетину діагоналей.
Означення. Квадрат — це прямокутник, в якого всі сторони рівні.
У квадрата всі сторони рівні, як у ромба, і всі кути прямі, як у прямокутника.
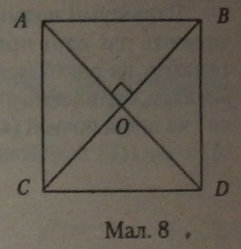
Властивості квадрата
1. Усі сторони рівні й попарно паралельні.
2. Усі кути прямі.
3. Діагоналі рівні й точкою перетину діляться пополам.
4. Діагоналі взаємно перпендикулярні та є бісектрисами кутів.
5. Точка перетину діагоналей є загальною вершиною 4 трикутників, що рівні між собою.
Автор: admin от 10-06-2013, 17:58, Переглядів: 43867