Вектор на площині

Вектор та його координати

Вектор — це напрямлений відрізок прямої. «Вектор» з латинської дослівно перекладається як «той, що везе», «той, що несе». Можна сказати, що вектор — це прямолінійний відрізок, якому надано певний напрям, що має початком точку (А), з якої він виходить, і кінцем — точку (В).

Вектор означає не тільки числове значення, але й напрям (мал. 45). Наприклад, вектором позначається швидкість, сила та інше.

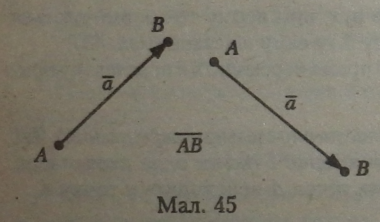
Вектор позначається як пряма лінія, латинською маленькою буквою, але з рискою над нею а __(в  деяких  позначеннях, ставлять

Над вектором стрілку). Правильним буде також позначення вектора за точками початку та кінця відрізка, але теж із спільною рискою над літерами АВ.

Вектор має абсолютну величину, яка є довжиною відрізка (в одиницях довжини), що зображує вектор. У декартовій системі координат довжина відрізка визначається як модуль відстані між точками по координатах початку і кінця відрізка.

Правило. Абсолютна величина вектора дорівнює модулю в*Д' стані між точками початку ft кінця вектора або довжині відріз**’

Вектори бувають однаково напрямленими (а і Ь ) і протилежно напрямленими(с id).

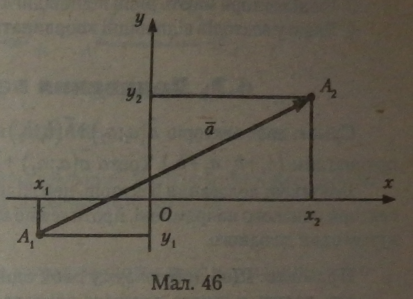Якщо початок вектора збігається з його кінцем, то такий вектор називають нульовим вектором ( 0 ). Про напрямлення нульового вектора не говорять, його абсолютна величина дорівнює 0. Розмістимо вектор а у системі координат (мал. 46).

Рівність векторів

Означення. Два вектори називають рівними, якщо їх можна сумістити паралельним перенесенням.

Паралельне перенесення дозволяє початок і кінець одного вектора перенести відповідно у початок і кінець другого вектора, не змінюючи абсолютну величину вектора та його напрямлення (мал. 47).

Правило. Рівні вектори однаково напрямлені й рівні за абсолютною величиною.

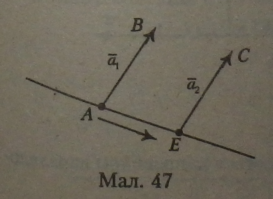
Якщо вектор ЛВ перенести паралельно та сумістити його з вектором ЕС, то вони збіжаться за абсолютною величиною і будуть однаково напрямлені (мал. 47).

Висновки з означення рівності векторів

1. Рівні вектори однаково напрямлені і рівні за абсолютною величиною.

2. Якщо вектори однаково напрямлені й рівні за абсолютною величиною, то вони рівні між собою.

3. Рівні вектори мають рівні відповідні координати.

4. Якщо у векторів відповідні координати рівні, то вектори рівні.

Додавання векторів

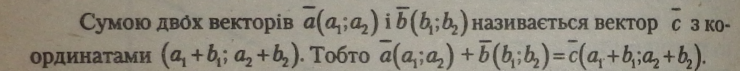
Вивчаючи додавання векторів, необхідно розглядати три випадки: вектори однаково напрямлені, протилежно напрямлені та розміщені під кутом один до одного.

Правило. Щоб добути суму двох однаково напрямлених векторів, досить у кінець першого вектора вмістити початок другого вектора (сумістити точки кінця і початку векторів) і одержати новий вектор, у якого початком буде початок першого вектора, а кінцем — кінець другого вектора.

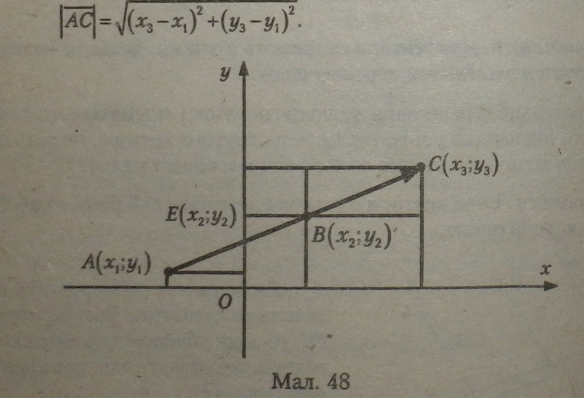
Додавання векторів однаково напрямлених зображено на мал. 48. У системі координат: АЕ + В С = АС, але за абсолютною величиною сумарний вектор дорівнює:

Вектори зі спільним початком складаються за правилом паралеле грама (мал. 49, а).

Правило. Для векторів із спільним початком їх сума зобр*3*^ ється діагоналлю паралелограма, побудованого на цих вектор як на сторонах.

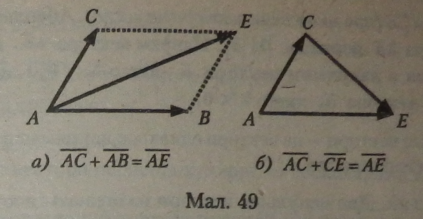
Теорема про додавання векторів: Які б не були точки Л, ВіС,

Справджується векторна рівність: АС+АВ = АЕ.

Висновки теореми

1.  Два довільних вектори можна замінити третім сумарним вектором трикутника (мал. 49, б).

2.  Два вектори, що мають спільний початок (мал. 49, а) у сумі є третім вектором, як діагональ паралелограма, побудованого на заданих векторах як на сторонах (правило паралелограма).

3.  Щоб побудувати вектор, рівний різниці заданих векторів, необхідно третій вектор розмістити так, щоб його початок збігся з кінцем вектора, який віднімаємо, а кінець — з кінцем вектора, від якого віднімаємо, попередньо обидва вектори перенести так, щоб у них була одна1 спільна точка початку векторів (мал. 49, б).

Множення вектора на число

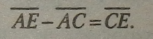
Теорема 38 (промноження вектора на число).

Колінеарні вектори — це вектори однаково напрямлені або напрямлені у протилежні сторони. .

Означення. Два ненульові вектори називаються колінеарними векторами, коли вони лежать на одній прямій або на двох паралельних прямих.

Скалярний добуток векторів

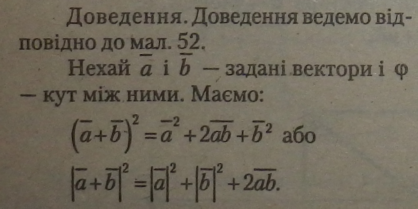
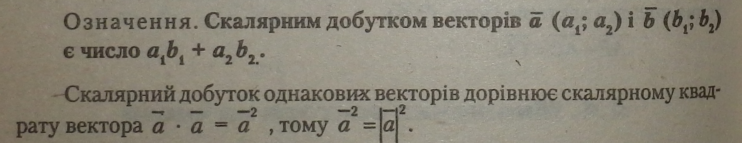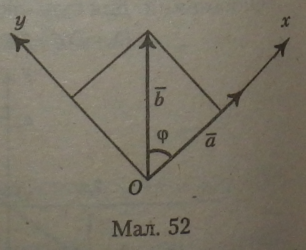
Теорема 40 (про скалярний добуток векторів). Скалярний добуток векторів дорівнює добутку їх абсолютних величин на косинус кута між ними.

З цього видно, що скалярний добуток ab не залежить від обраної системи  і t

Координат. Оберемо її так, як показано на малюнку. Тоді вЄКЩЩ]| будуть мати координати:

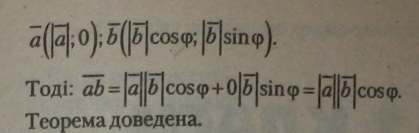Висновки теореми: 1.  Якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю. 2.  Якщо скалярний добуток векторів, відмінних від нуля, дорівнює нулю, то вектори перпендикулярні. 3.  Сума квадратів діагоналей паралелоірама дорівнює сумі квадратів його сторін.  .

Одиничний вектор

Означення. Одиничним називається вектор, абсолютна величина якого дорівнює одиниці.

Одиничні вектори, які мають напрями додатних координатних пів - осей, наливаються координатними векторами або ортами.