Синус, косинус, тангенс кутів від 0° до 180°, Перетворення геометричних фігур, симетрія відносно точки та прямої

Синус, косинус, тангенс кутів від 0° до 180°

Визначити значення синуса, косинуса та тангенса кутів від 0е до 180° можна за допомогою одиничного кола, вміщеного в систему координат так, щоб центр кола збігався з початком координат (мал. 39).

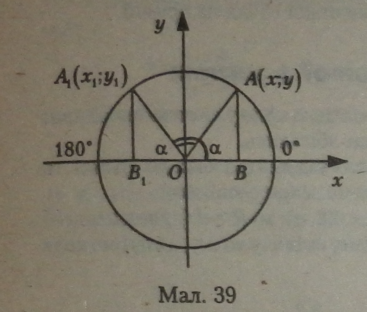
Якщо х і у — координати точки А, то тригонометричні функції гострого кута а визначаються за такими формулами:

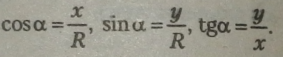
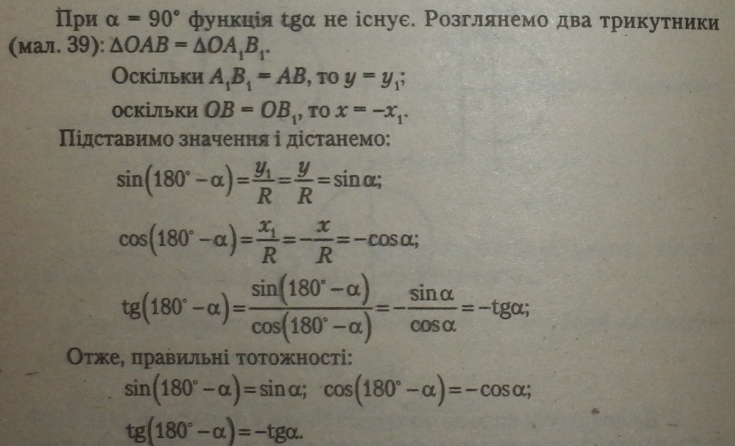
За цими формулами можна обчислити будь-яку тригонометричну функцію тупого кута за тригонометричною функцією гострого кута.

Перетворення геометричних фігур

Означення. Якщо кожну точку геометричної фігури змісти™ на певну відстань в одному напрямі, то дотанемо нову фігуРУ* рівну даній. Про нову фігуру говорять, що вона утворилася перетворенням із даної фігури. Перетворення однієї фігури на інДОУ називають рухом, якщо воно зберігає відстань між точкам:

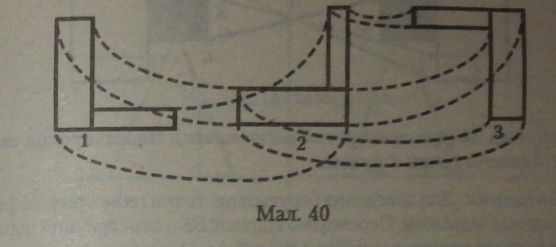
Перетворення фігури 2 у фігуру 3 — це теж рух.

Перетворення фігури 1 у фігуру 3 — це теж рух (можна оминути рух

2 як етап).

Теорема 33. При русі Точки, що розміщені на прямій, перехода» у точки, що розміщені на прямій, і зберігається яоржяак їх взаємного розміщення.

Висновки теореми

1. При русі  прямі переходять у прямі, ггівпрямі — у півпрямі, відрі ищ — У Відрізки.

2. При русі зберігаються кути між півпрямимн.

Симетрія відносно точки

Означення. Симетрія відносно даної точки - це перетворення при якому кожна точка фігури нереходть у сжшг рттку В ку відносно даної точки.

Точка В називається симетричною точці С відносно центра сжмирв А, якщо Відрізок ВС проходить через центр А І ЛІПИТЬСЯ дш цевтрвм пополам: АВ - АС (мал. 41).

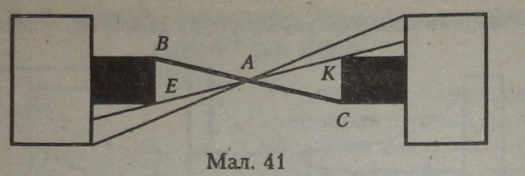
Теорема про симетрію відносно точки: Перетворення симетрії відносно точки є рухом.

Доведення. Для доведення беруться дві точки геометричної фігури і сполучаються відрізком. Переведемо відрізок BE в симетричний відносно точки, для цього сполучимо центр симетрії А з даними точками прямими лініями і на продовженні прямих відкладемо відрізки, рівні відрізкам від даної точки до центра симетрії. Одержимо в точках на продовженні прямих (при їх сполученні) кінець і початок нового відрізка КС, симетричного даному (мал. 41).

Для доведення симетричності відрізка відносно точки А розглянемо два трикутники (АВАЕ і АКАС) із спільною вершиною в центрі симетрії. Вони рівні між собою за першою ознакою рівності трикутників.

Отже, відрізок BE, який сполучає задані точки фігури, дорівнює відрізку КС, одержаному побудовою.

Наша побудова для доведення теореми повністю відповідає висновку 1 теореми 33.

Симетрія відносно прямої

Означення. Симетрія геометричної фігури відносно прямої — це таке перетворення фігури, коли кожна точка однієї фігури знаходиться на такій самій відстані від прямої, яка називається віссю симетрії, що й симетрична їй точка другої фігури. Відстань вимірюється по перпендикуляру до осі симетрії.

Обидві фігури розміщені в різних півплощинах від осі симетрії (прямої) і, якщо перегнути площину по осі симетрії, то симетричні фігури повністю збігаються (мал. 42).

Теорема про симетрію відносно прямої: Перетворення симетрії відносно прямої є рух.

Доведення. Для доведення розмістимо точки заданої геометричної фігури в декартовій системі координат і знайдемо їх координати. За вісь симетрії приймемо вісь ординат (мал. 42).

Опустимо перпендикуляр із заданої точки на вісь ординат та на його продовженні відкладемо такий самий відрізок. Координати одержаної точки кінця побудованого відрізка будуть відрізнятись від координат заданої точки тільки знаком абсциси.

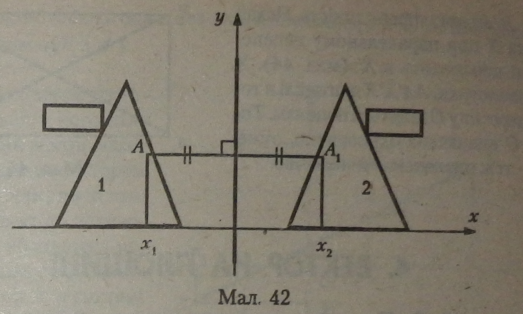
Подібно до теореми 34 ми одержали перетворення заданих ючок другого квадранта в першому квадранті, тобто наша побудова є рух точок відносно прямої (осі ординат).

Паралельне перенесення та його властивості

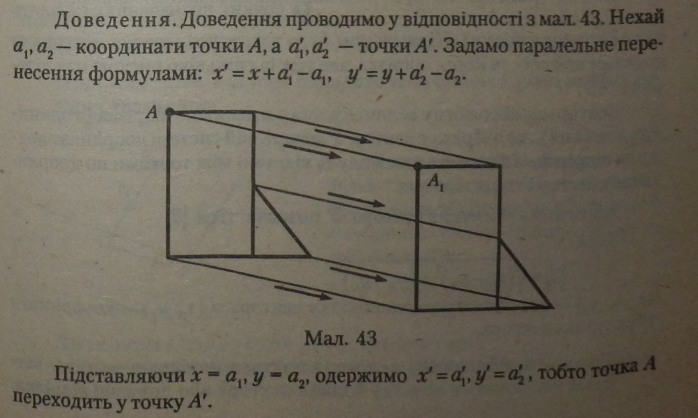
Паралельне перенесення — це рух, при якому точки зміщуються вздовж паралельних прямих на одну й ту саму відстань (мал. 43).

При паралельному перенесенні пряма переходить в паралельну пряму, тобто самая себе.

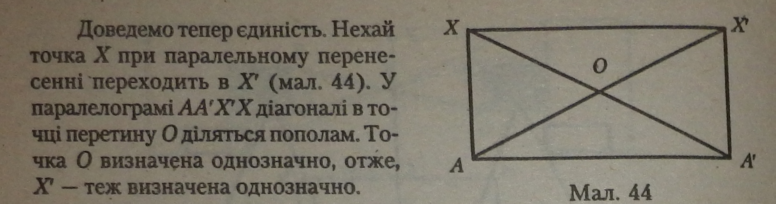
Теорема 36 (про існування іединість паралельного перенесення). Які б не були дві точки А і Alt існує одне і тільки одне паралельне перенесення, при якому задана точка А переходить у точку At.