Рівняння кола, координати точки перетину двох прямих, перетин прямої з колом

Рівняння кола

Коло — це геометричне місце точок з однією визначеною властивістю (кожна точка кола рівновіддалена від однієї точки, що називається центром). Рівняння кола повинне відбивати цю властивість, задовольняти цю умову.

Геометрична інтерпретація рівняння кола — це коло.

Якщо помістити коло в систему координат, то всі точки кола задовольняють одну умову — відстань від них до центра кола повинна бути однаковою і дорівнюватиме радіусу кола.

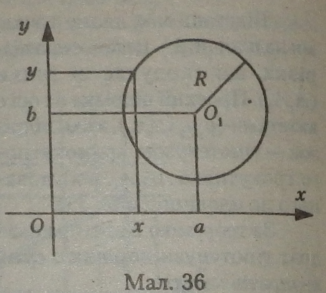
Коло з центром у точці А і радіусом R помістимо в координатну площину (мал. 36).

Якщо координати центра (a; b), а координати будь-якої точки кола (*; У), то рівняння кола має вигляд:

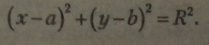
Означення. Якщо сума квадратів ріаниць відповідних координат будь-якої точки кривої і деякої точки Ц на координатнії

Площині постійна, то ця крива — коло, точка О, — його центр, а сума — квадрат його радіуса.

Якщо центр кола збігається з точкою початку координат, то квадрат радіуса кола дорівнює сумі квадратів координат будь-якої точки кола У цьому випадку рівняння кола набуває вигляд: х2 +у* = R2.

Отже, будь-яка геометрична фігура як геометричне місце точок визначається рівнянням, що зв’язує координати її точок. І навпаки, рівняння, що зв’язує координати х і у, визначає лі-нію як геометричне місце точок площини, координати яких задовольняють дане рівняння.

Координати точки перетину двох прямих

Означення. Якщо дві прямі перетинаються (мають спільну точку), то координати точки перетину повинні задовольняти обидва рівняння прямих.

Рівняння прямої в плоскій системі декартових координат має такий загальний вигляд: ах + by + с * 0.

Розміщення прямої на площині в декартовій системі координат

Розміщення прямої на площині в системі координат — це варіанті можливого розміщення відносно осей координат і по квадрантах (з’ясо вується шляхом аналізу рівняння прямої в загальному вигляді). Ми мо жемо з’ясувати з конкретного рівняння: перетинає чи ні пряма осі коор динат; проходить чи ні через точку початку координат, що впливає ні нахил прямої до осей і як.

Вивчивши цю тему, можна схематично зобразити пряму за її рів нянням на координатній площині (без обчислень двох точок прямої).

Кутовий коефіцієнт у рівнянні прямої

Означення. Кутовий коефіцієнт — це коефіцієнт (k) у зведено му рівнянні прямої (у ш kx +1). Кутовий коефіцієнт з точністю Д знака дорівнює тангенсу гострого кута, що утворює пряма з вк сю х.

З прямокутного трикутника, що складається з відрізка прямої TS його проекцій на осі, відношення різниці координат по осях — де відношення катетів, тому за означенням функції тангенса можна записати: ?=tga.

Знак кутового коефіцієнта додатний, тому що кут а в системі координат гострий (пряма належить І та III квадрантам при І “ 0).

2. Розглянемо рівняння прямої Я З kx + і Запишемо координати точок D (ж3; у3) і F(xa; у4), при цьому 9 > Я Оскільки обидві точки нале-жать одній прямій, то їхні координати задовольняють рівнянням

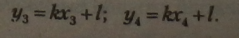
Ми з’ясували, що рівняння прямої в загальному вигляді записується повним рівнянням як: ах + by + с * 0.

Розглянемо окремі випадки неповних рівнянь прямої.

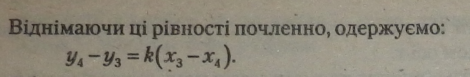Обчислимо кутовий коефіцієнт через координати двох точок на прямій:

1. Якщо а і 0, а b Щ 0, то рівняння прямої має вид:

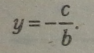
У рівнянні прямої відсутній х, тому рівняння буде правильною рівністю при будь-яких*у будь-якій точці на прямій.

У рівнянні прямої відсутній у, тому рівняння буде правильною рівністю при будь-яких у у будь-якій точці на прямій.

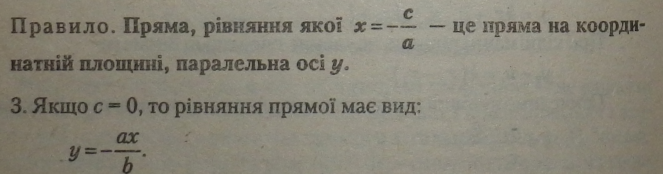Це рівняння прямої пропорційності і пряма пройде через точку початку координат (х - 0, у - 0).

Висновки 1.  Для побудови прямої в координатній площині за певним чи звед ним рівнянням досить знайти координати двох точок прямої. 2.  Для побудови прямої в координатній площині за повним чи звеД

Ним рівнянням досить знати координату одної точки і кутовий коефіцієнт (за таблицями визначається кут нахилу до осі д:).

3. Для побудови в координатній площині прямої за неповним рівнянням досить знати координати тільки одної точки на прямій.

Перетин прямої з колом

Візьмемо пряму лінію і коло. Розмістимо коло у системі координат так, щоб центр кола і початок координат збігались.

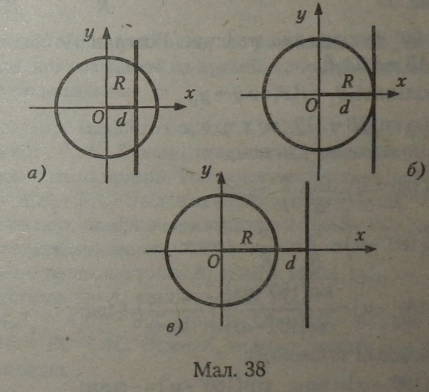
Якщо R — радіус кола, a d — відстань від центра кола до прямої, то взаємне розміщення кола і прямої може мати три розв’язки.

1. Якщо пряма перетинає коло (мал. 38, а), то R > d (пряма перпендикулярна до радіуса кола і має з ним одну спільну точку, а з дугою кола

2.  Якщо пряма, і коло дотикаються тільки в одній точці (мал. 38, б), то R = d (пряма, перпендикулярна до радіуса кола в точці дотику, є дотичною до кола, паралельна вертикальній осі кола). 3.  Якщо пряма і коло не мають спільних точок (мал. 38, в), то R < d (пряма знаходиться на відстані (d - R) від кола).

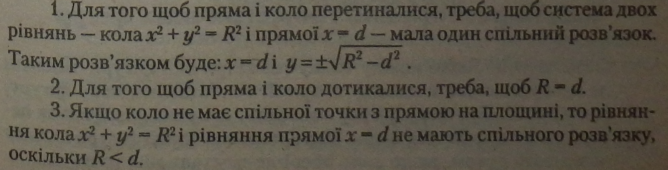— дві спільні точки).