Основні тригонометричні тотожності, значення синуса, косинуса і тангенса деяких кутів

Основні тригонометричні тотожності

Знаючи одну зі сторін прямокутного трикутника й один із його гострих кутів, можна визначити всі інші елементи трикутника (мал. 24).

1.  Катет, протилежний куту а, дорівнює добутку гіпотенузи на синус а.

2.  Катет, прилеглий до кута а, дорівнює добутку гіпотенузи на косинус а.

3.  Катет, протилежний куту а, дорівнює добутку другого катета на тангенс а.

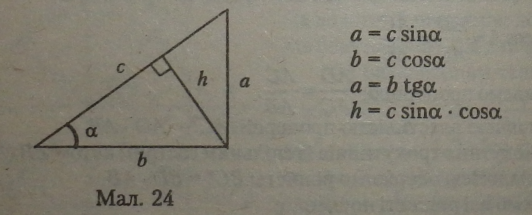
4. Висота прямокутного трикутника Л, опущена з прямого кута на гіпотенузу, дорівнює добутку трьох множників: гіпотенузи, синуса а і косинуса а.

Якщо є три відрізки, то не завжди можна одержати з них триланко-ву замкнену ламану (трикутник).

Теорема ЗО (про можливість і неможливість побудови трику тни' ка). Які б не були три точки, відстань між будь-якими двома з Щ точок не більша від суми відстаней від них до третьої точки.

Доведення деталізує умова теореми для трьох варіантів розташування точок: 1) дві або три точки збігаються; 2) три точки різні і лежать на одній прямій; 3) усі три точки не лежать на одній прямій.

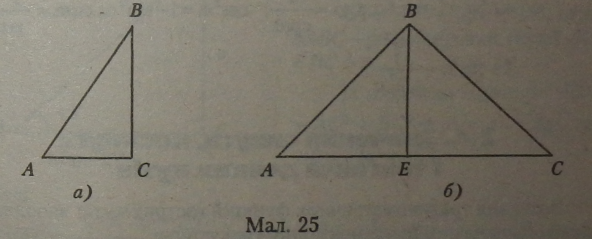
Тільки третій варіант (якщо три точки не збігаються і не лежать на одній прямій) передбачає побудову трикутника за трьома точками, як вершинами трикутника (мал. 25).

Доведення ґрунтується на розв’язуванні чітких алгебраїчних нерівностей і застосуванні теореми Піфагора (гіпотенуза завжди більша від катета).

Якщо три точки збігаються, то твердження теореми очевидне.

Якщо збігаються дві точки, то одержуємо відрізок, один кінець якого складають дві точки, що збігаються, і твердження теореми також очевидне.

Якщо три точки різні і лежать на одній прямій, то одна з них лежить між двома іншими, у цьому випадку більший із трьох відрізків дорівнює сумі двох інших (аксіома 3).

Доведення.«Розглянемо варіант, коли три точки не лежать на одній прямій (мал. 25) для двох варіантів сполучення цих точок — прямокутний трикутник (мал. 25, а) і гострокутний чи тупокутний трикутник (мал. 25, б).

Висновки теореми

1.  У будь-якому трикутнику кожна сторона менша від суми двох інших.

2.  Будь-яка хорда кола менша чи дорівнює діаметру кола.

3.  Якщо відстань між центрами двох кіл більша за суму їхніх радіусів, то кола не дотикаються і не перетинаються між собою.

Основні тригонометричні тотожності:

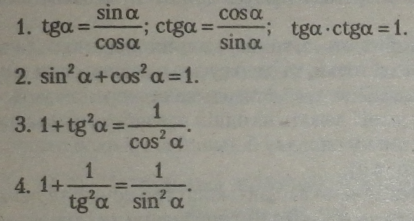З основних тригонометричних тотожностей випливають такі тотожності:

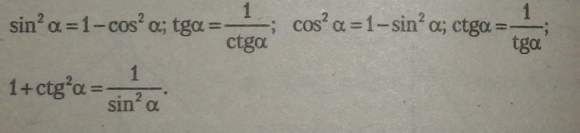
Значення синуса, косинуса і тангенса деяких кутів

Значення тригонометричних функцій гострих кутів виводяться із співвідношення сторін прямокутного трикутника.

Розглянуті нами функції кутів у розділі 2.1 на прикладі одиничного кола використаємо для обчислення тригонометричних функцій, винося-чи отримані прямокутні трикутники (мал. 19,20,22) за коло і систему координат.

Теорема 31 (про значення синуса, косинуса і тангенса деяких кутів).

Знайдемо значення тригонометричних функцій при а ¦ 45*.

Знайдемо значення тригонометричних функцій при а ¦ ЗО*.

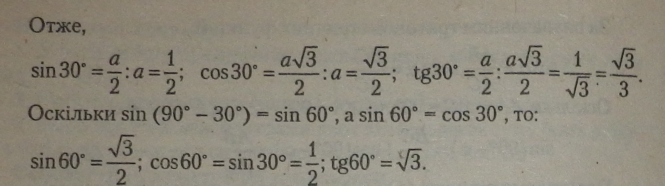У загальному вигляді зміни тригонометричних функцій зі зростанням кута наведено в теоремі 32.

Теорема 33 (про зміни функцій синуса, косинуса і тангенса при зростанні кута). При зростанні гострого кута функції sina, tga зростають, а функція cosa спадає.