Теорема Фалеса, середня лінія трикутника

Теорема Фалеса

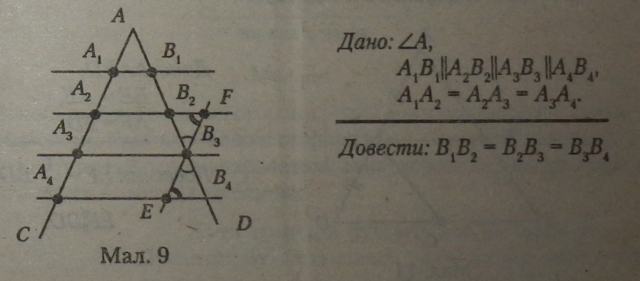
Теорема Фалеса розглядає кут як дві прямі зі спільною точкою, що перетинаються кількома паралельними прямими (мал. 9). Теорема доводить рівність між собою відрізків на кожній стороні кута, що лежать між паралельними прямими.

Теорема 24 (теорема Фалеса). Якщо паралельні прямі, що перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні.

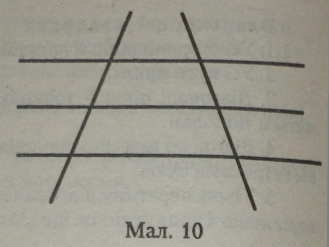
Висновок теореми для будь-яких двох прямих Паралельні прямі, що перетинають дві дані прямі й відтинають на одній прямій рівні відрізки, відтинають рівні відрізки і на іншій прямій (мал. 10).

Середня лінія трикутника

Означення. Середня лінія трикутника — це відрізок, що сполучає середини двох його сторін.

На основі теореми Фалеса можна визначити середню лінію трикутника, якщо розглядати сторони трикутника як дві дані прямі, а основу і середню лінію трикутника як паралельні прямі (мал. 11).

Теорема 25 (про середню лінію трикутника). Середня лінія трикутника, яка сполучає середини двох даних сторін, паралельна третій стороні й дорівнює її половині.

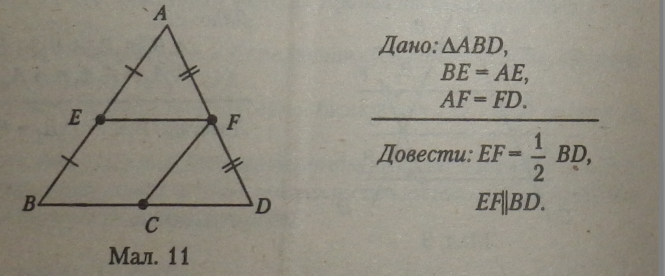
Доведення. EF— середня лінія ZABD.

1)  Через точку / проведемо пряму, паралельну стороні BD. За теоремою Фалеса вона перетинає відрізок АВ у його середині (точці Е), тобто містить середню лінію EF. Отже, середня лінія /^паралельна стороні BD.

2)  Проведемо середню лінію FC. Вона (доведено вище) буде паралельна АВ.