Теорема піфагора

Теорема 29 (теорема Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

Доведення теореми Піфагора здійснюється за допомогою теореми про косинус кута (теорема 28).

Висновки теореми 1. У прямокутному трикутнику кожний з катетів менший від гіпотенузи. Якщо до прямої з однієї точки проведені перпендикуляр і похила, то будь-яка похила більша від перпендикуляра.

2.  Косинус кута менше 1 (одиниці) для будь-якого гострого кута.

3.  Для будь-якого рівнобедреного трикутника з основою а і сторонами Ь висота Л, проведена до основи, дорівнює кореню квадратному з різ-ниці квадратів бічної сторони і половини основи трикутника:

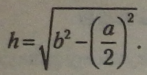
4. Рівні похилі мають рівні проекції, із двох похилих більша та, у якої проекція більша.

У висновку 4 похилі варто розглядати як гіпотенузи двох прямокутних трикутників, у яких одна спільна сторона (висота третього трикутника), а другі катети служать проекціями гіпотенуз і є взаємно доповняльними прямими (мал. 23).