Основи тригонометрії, синус, косинус і тангенс гострого кута прямокутного трикутника
Тригонометрія — розділ математики, що вивчає тригонометричні функції і їхнє застосування в розв’язуванні задач, головним чином геометричних.
Основна задача тригонометрії — розв’язування трикутників, тобто обчислення невідомих величин трикутника через його відомі величини.
Будь-яку геометричну задачу можна звести до розв’язування за допомогою трикутників, тому тригонометрія застосовується й у планіметрії (вивченні плоских геометричних фігур), і в стереометрії (вивченні просторових геометричних фігур). Будь-яка тригонометрична величина є функція кута (змінюється зі зміною кута), тому і з’явилася назва «тригонометричні функції».
Тригонометричні функції—функції кута: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec) і косеканс (cosec).
Обернені тригонометричні функції, чи кругові функції, — арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) і арккотангенс (arcctg).
Прямі функції кута використовують, коли за кутом знаходять функцію, а обернені — коли за функцією знаходять кут.

Розглянемо тригонометричні функції кутів на прикладі одиничного кола (коло, радіус якого дорівнює 1). Якщо намалювати коло з г-1 і одну сторону кута позначити як радіус О А (мал. 18) і прийняти його за нерухому сторону кута (закріпити О А), другий радіус можна назвати рухомим (ОВ) і прийняти його за другу (рухому) сторону кута. Коло потрібно помістити в плоску систему координат так, щоб центр кола збігався з початком координат.
Рухаючи рухомий радіус за повним колом проти годинникової стрілки, ми будемо збільшувати кут від 0е (коли рухома сторона кута збігається з нерухомою, тобто точка В збігається з точкою А) до 360е (обійшовши коло, рухомий радіус ОВ знову збігатиметься з нерухомим радіусом ОА).
Якщо рухомий радіус (ОВ) знаходиться в І квадранті — одержуємо гострі кути (від 0* до 90е); збігається з додатною піввіссю у — прямий кут (90*); знаходиться в II квадранті — тупі кути (від 90е до 180е); збігається з від’ємною піввіссю х—розгорнутий кут (180е); знаходиться в III кваД' ранті — кути від 180е до 270*; збігається з від’ємною піввіссю у — кут 270» знаходиться в IV квадранті - кут від 270е до 360е.
Синус кута — це тригонометрична функція кута, що позначається як sin. Дослівно перекладається з латинської як «вигин, кривизна».
Рухаючи рухомий радіус за повним колом за годинниковою стрілкою, ми одержуємо від’ємні кути, від 0° до -360е.
Означення. У прямокутному трикутнику сторона, протилежна прямому куту, називається гіпотенузою, а інші сторони — катетами.
Означення. Синус гострого кута в прямокутному трикутнику є відношення протилежного катета до гіпотенузи.

 |
|
Отже, синус кута — це величина проекції рухомого відрізка В С на вісь у. |
Розглянемо на колі зміни функції синуса гострого кута, побудувавши на нерухомій стороні кута (ОА) катет прямокутного трикутника (ОС), у якого гіпотенузою буде рухомий радіус (ОВ) (мал. 19).
Розглянемо зміни функції sina (відрізка ВС) при русі рухомого радіуса по колу і збільшенні кута. Межі зміни синуса кута будемо визначати за квадрантами.

За пройдене перше півколо sina змінився від 0 до 0, а найбільше його значення, що дорівнює 1, збігається з довжиною радіуса на додатній півосі у.
Друге півколо руху рухомого радіуса можна розглядати як додатний напрямок (при русі ОВ далі проти годинникової стрілки) і як від’ємний* напрямок (якщо ОВ обертати за годинниковою стрілкою). Розглянемо тільки додатний напрямок.

За пройдене друге півколо sina змінився від 0 до 0, а найменше його значення, що дорівнює -1, збігається з довжиною радіуса на від’ємній півосі^. * -
За весь оберт рухомого радіуса ОВ, від збігу з О А другого їхнього збігу, кут чисельно змінився від 0° до 360°, а числове значення синуса кута змінилось у межах від 1 до -1.
Друга тригонометрична функція — косинус кута, що позначається як cos.
Означення. Косинус кута — це відношення прилеглого катета прямокутного трикутника до гіпотенузи.
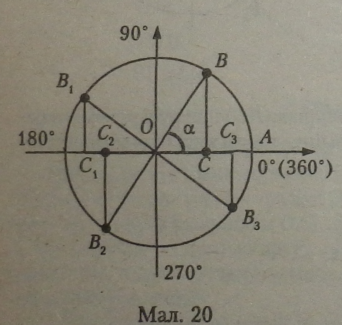
Косинус кута позначається як cosa.
Розглянемо по квадрантах зміни функції косинуса кута а при тому самому русі рухомого радіуса ОВ по колу від 0° до 360° (мал. 20).
|
За визначенням косинуса кута: |
 |
Розмір відрізка ОС змінюється (у межах кола) на осі ху залежності від розміщення рухомого радіуса (величини кута).
Розглянемо зміни функції cosa (відрізка ОС) при русі рухомого раді* уса по колу й збільшенні кута. Межі зміни косинуса кута будемо визначати по квадрантах.

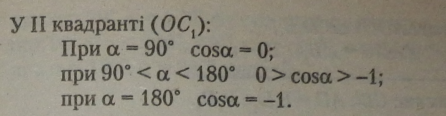
За пройдене рухомим радіусом (ОВ) перше півколо cosa змінився від 1 до -1 > найбільше й найменше його значення збігаються з довжиною радіуса на додатній і від’ємній півосях х.
Друге півколо руху рухомого радіуса можна розглядати як додатний напрямок (при русі ОВ далі проти годинникової стрілки) і як від’ємний напрямок (якщо ОВ обертати за годинниковою стрілкою). Розглянемо тільки додатний напрямок.
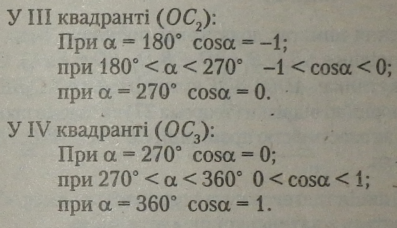
За пройдене друге півколо cosa змінився від -1 до 1, найменше й найбільше його значення збігаються з довжиною радіуса на від’ємній і додатній півосі х.
За весь оберт рухомого радіуса ОВ, від збігу з О А до другого їхнього збігу, кут чисельно змінився від 0° до 360°, а числове значення косинуса кута змінювалося в межах від 1 до -1.
Числове значення синуса і косинуса кута залежить тільки від градусної міри кута і не залежить від параметрів прямокутного трикутника і його розміщення на площині. Функції синуса й косинуса кута в числовому значенні не перевищують ±1.
Цей висновок доводиться теоремою 28. Обчислити значення синуса і косинуса будь-якого гострого кута прямокутного трикутника завжди можна, якщо відомі довжини його катетів і гіпотенузи, але частіше обчислення не проводять, а зчитують значення функцій за таблицями логарифмів тригонометричних функцій у залежності від величини гострого кута.
Теорема 28 (про косинус кута). Косинус кута залежить тільки від градусної міри кута й не залежить від розміщення і розмірів прямокутного трикутника.

Тригонометрична функція тангенса кута позначається як tg. «Тангенс» дослівно перекладається з латинської як «дотичний».
Означення. Тангенс гострого кута прямокутного трикутника є відношення протилежного катета до прилеглого катета.

Лінія тангенсів — це дотична / до одиничного кола в точці А (1; 0). За додатний напрямок лінії тангенсів беруть напрямок знизу вгору.
За визначенням тангенса кута:

Тангенсів. Інакше кажучи, тангенс кута — це величина відрізка дотичної, проведеної через точку А (кінець нерухомого радіуса), від точ-:и доти*
Ку А до перетину з продовженням рухомого радіуса ОВ.
Розглянемо зміну величини tga (відрізка АС) при русі рухомого радіуса ОВ по колу і збільшенні кута. Відзначимо, що значення tga збігаються у І і III квадрантах, у II і IV квадрантах:
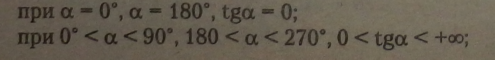

Автор: admin от 10-06-2013, 18:36, Переглядів: 17845