5. Суміжні кути та їхні властивості

(2 год, уроки № 9, 10)

КОМЕНТАР ДЛЯ ВЧИТЕЛЯ

У результаті вивчення § 5 учні мають: знати: означення суміжних кутів, теорему про суму суміжних кутів та наслідки з неї (із доведенням); зміст понять «наслідок» та «посилання»; уміти: будувати кут, суміжний із даним; знаходити суміжні кути на готовому рисунку; доводити теорему про суму суміжних кутів та наслідки з неї; використовувати ці твердження для обґрунтування розв'язування задач (на суміжні кути).

1. Введення означення суміжних кутів автори підручника мотивують необхідністю розглянути окремі випадки взаємного розміщення двох кутів зі спільними елементами.

Також важливо звернути увагу на необхідність точного відтворення учнями означення суміжних кутів: щоб переконати в цьому, можна після введення означення суміжних кутів запропонувати завдання.

Завдання. Чи є суміжними кути, позначені на рис. 1? Чому?

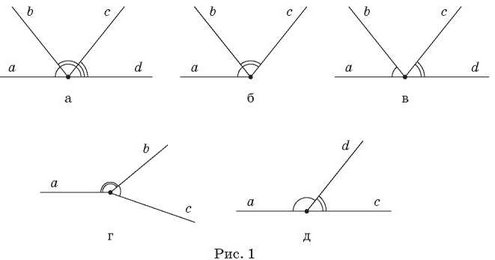
Опрацювавши з учнями означення суміжних кутів, бажано розібрати технологію побудови кута, суміжного з даним.

2. Оскільки теорема про суму суміжних кутів є досить простою і доведення її ґрунтується на аксіомі вимірювання кутів, можна запропонувати учням опрацювати її доведення самостійно.

Важливо попередити традиційну помилку учнів: твердження, обернене до зазначеної теореми, не є правильним. При цьому вводити поняття «обернене твердження» не обов’язково, адже воно докладно розглядатиметься в п. 11.4.

3. Залежно від рівня підготовки учнів та сформованості навичок їх самостійної діяльності, формулювання і доведення наслідків із теореми про суміжні кути або може здійснити сам учитель, або учні працюватимуть із текстом підручника самостійно, або можна організувати практичну роботу в групах, що дозволить учням здійснити «відкриття» ними самими сформульованих і доведених у підручнику наслідків із теореми про суму суміжних кутів.

Тема «Суміжні кути» розглядається в підручнику в межах традиційного підходу. Після введення означення суміжних кутів варто приділити увагу важливості кожного слова в цьому означенні (навести необхідні контрприклади або запропонувати учням зробити це самостійно). Звертаємо увагу на наслідки з теореми про суміжні кути і тлумачення понять «наслідок» і «посилання», подане в п. 5.2. Можна запропонувати учням самостійно сформулювати інші наслідки з доведеної теореми на основі розв’язання усних задач цього параграфа. У процесі розв’язування задач із метою економії навчального часу рекомендуємо використовувати задачі на готових кресленнях (зокрема, задачі самостійної роботи 4 посібника [3], який входить до навчально-методичного комплекту нашого підручника).

ПЛАНУВАННЯ ВИВЧЕННЯ МАТЕРІАЛУ

На вивчення § 5 відводиться два уроки.

На першому уроці:

у класі: провести самостійну роботу за попередньою темою як перевірку домашнього завдання (див. нижче); вивчити означення суміжних кутів; сформулювати й довести теорему про суму суміжних кутів та розв’язати вправи: усні вправи 1-3 (с. 35);

[2]: № 115 графічно; № 117, 119, 121 письмово; додаткову задачу 1 (с. 37) усно; вдома [2]: § 5, п. 5.1, 5.2 (перша частина, до наслідків); повторити види кутів за їх градусною мірою; розв’язати вправи:

[2]: № 110, 112-114 усно, № 118, 120, 123 письмово.

На другому уроці:

у класі: провести математичний диктант (с. 36); сформулювати й довести наслідки з теореми про суму суміжних кутів і розібрати зміст понять «наслідок» та «посилання»; розв’язати вправи: усні вправи 4-8 (с. 36);

[2]: № 124, 125, 127, 129 письмово; додатково № 131; вдома: [2]: § 5, п. 5.2 (друга частина); розв’язати вправи:

[2]: № 113, 114 усно; № 126, 128 письмово; № 134, 135 на повторення;

додаткову задачу 2 (с. 37) усно.

ВКАЗІВКИ ДО РОЗВ’ЯЗУВАННЯ ЗАДАЧ

При розв’язуванні задач № 115, 117, 119, 121 слід робити посилання на означення суміжних кутів та теорему про суму суміжних кутів.

Розв’язувати задачі № 124, 125, 127, 129 слід із посиланням на відповідний наслідок із теореми про суму суміжних кутів.

Розв’язування задачі № 131 надає учням опорний факт, який може надалі використовуватися для розв’язування задач: кут між бісектрисами суміжних кутів — прямий.

Самостійна робота

За посібником [3]:

Самостійна робота 4: задача 2 (варіанти 1, 2); самостійна робота 5: задача 2 (варіанти 1, 2); самостійна робота 6: задача 3 (варіанти 1, 2)

або за посібником [4]:

Самостійна робота № 2.

Усні вправи

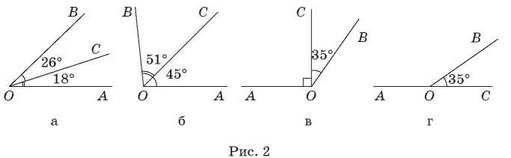
1. Знайдіть градусну міру кута AOB, зображеного на рис. 2, а-г.

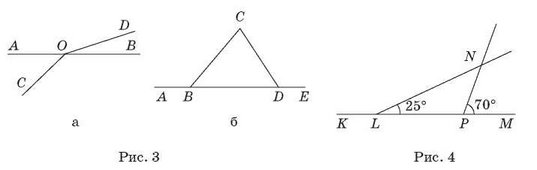
2. Чи є на рис. 3, а, б пари суміжних кутів?

3. Знайдіть градусні міри кутів KLN і LPN (рис. 4).

4. Яке з чисел

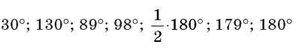
є градусною

мірою:

а) тупого кута;

б) гострого кута;

в) прямого кута;

г) розгорнутого кута?

5. Скільки градусів може становити сума:

а) двох прямих кутів;

б) двох гострих кутів;

в) двох тупих кутів;

г) прямого й гострого кутів?

6. Знайдіть кут X на рис. 5.

Математичний диктант

1. Накресліть від руки два нерівні суміжні кути так, щоб їхня спільна сторона була розміщена горизонтально [вертикально].

2. Накресліть два суміжні кути так, щоб їх сторони, що є доповняльними променями, були розміщені вертикально [горизонтально].

3. Накресліть два кути, які не є суміжними, так, щоб вони мали одну спільну сторону й обидва були тупими [гострими].

4. Побудуйте кут AOB, що дорівнює 70° [60° . Накресліть і позначте два кути, кожний з яких є суміжним із даним кутом. Знайдіть градусні міри цих кутів.

5. Знайдіть кут, суміжний із даним кутом, і запишіть види кутів у кожній парі:

а) 30° [140°]; б) 90° [50°].