Паралельність прямих

Теорема про паралельність прямих: Дві прямі, паралельні третій, паралельні між собою.

Дано три прямі a, b, с. Прямі а і b паралелені прямій с. Довести, що a і b - паралельні (мал. 39, в). Доведення Доведемо теорему способом від супротивного. Припустимо, шо а і b перетинаються в певній точці А (мал. 39,б)

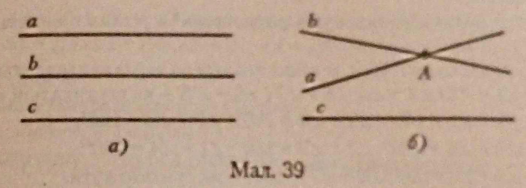За аксіомою 9 через точку. A, яка лежить поза прямою с, можна про вести тільки одну пряму, паралельну їй. Отже, за нашим припущенням тільки одна з двох прямих a або b може бути паралельна с. Наше припущення неправильне, тому що супе речить умові теореми. Отже, висновок теореми правильній і дійсно - a||b

При перетині двох прямих третьою прямою завжди утвориться вісім кутів (мал, 40) Існує два варіанти взаєморозміщення прямої і січної:

• прямі не паралельні (мат 40, а);

0 прямі паралельні (мал. 40, ?)

Кути 1-8 мають спеціальні назви, а величини цих кутів визнача-ються положенням прямих (паралельні прямі чи ні)

1.  Внутрішні односторонні кути - це кути 3 і 6.4 і 5.

2. Зовнішні односторонні кути - це кути 2 і 7,118.

3.  Внутрішні різносторонні куш * це кути 3 і 5,4 і 8.

4.  Зовнішні різносторонні кути - це 2 і 8, t і 7*

5.  Відповідні кут и це 2 і 6.1 і 5,317, і і 8.

2.6. Ознака паралельності прямих

Щоб перевірити, чи паралельні прямі, достатньо знати градусну міру двох різмостором иіх кутів, або двох відповідних кутів, або суму двох односторонніх кутів.

Теорема 12 (ознака паралельності прямих). Якщо внутрішні різ иосторонні кути рівні або сума внутрішніх односторонніх кутів дорівнюс 180", то прямі паралельні.

Дано три прямі о, Ь, с. Пряма с — січна. Довести, щ0 а§А (мал. 40, б).

Доведення. Виконується доведення теореми методом від супротивного (мал. 42). Припустимо, що а не паралельна Ь, тоді вони перетинаються в певній точці С.

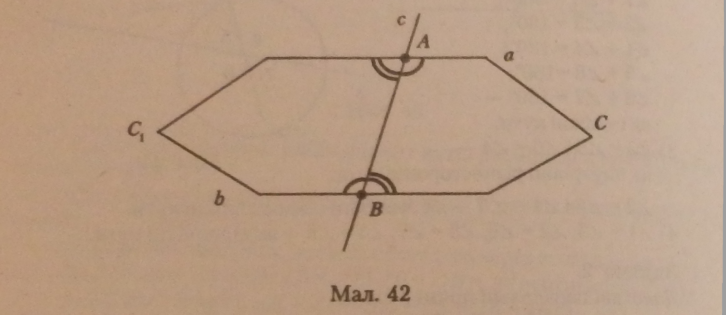Оскільки різносторонні кути рівні, то АЛВС - ДABCV а в рівних трикутниках проти рівних кутів лежать рівні сторони, отже, пряма АС збігається з прямою а, а ВС{ — з прямою Ь. Через дві точки Сі С. проходять дві різні прямі а і Ь, тобто вони збігаються, що суперечить умові теореми. Отже, наше припущення неправильне, і прямі а і Ь—паралельні.

Висновки теореми 12

1.  Дві прямі, перпендикулярні третій, паралельні

2.  Прямі паралельні, якщо відповідні кути рівні.

Задача 1 (проможливість провести через точку, яка не належить прямій, пряму, паралельну даній).

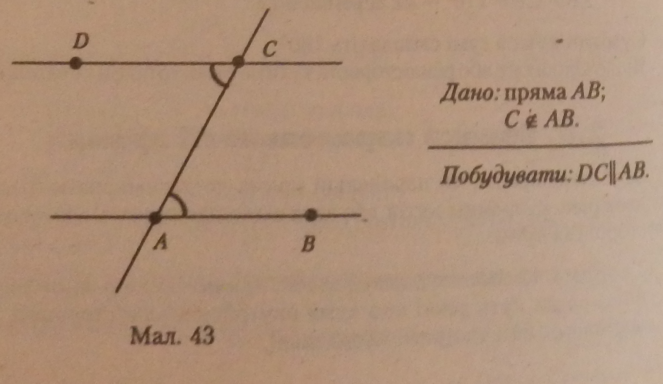
Розв язання. Через точку Сі приму АВ проведемо пряму АС.

Пряма АС розбиває площину на дві півплощиии. /МАВ лежить в ОДНІЙ иівплощині відЛС. Побудуємо рівний йому кут з вершиною в точці С в другій иівплощині від А С. Сторона DC другого кута буде паралельна АВ, оскільки /САВ * /А CD (за побудовою), а ці кути внутрішні різно-сторонні при січній АС.

Отже, щоб побудувати пряму, паралельну заданій, і таку, що проходить через точку поза прямою, достатньо побудувати рівні різносторонні кути при січній.

Висновки задачі 1 І аксіоми 9

Через точку, яка не лежить на даній прямій, можна провести паралельну їй пряму, і тільки одну.

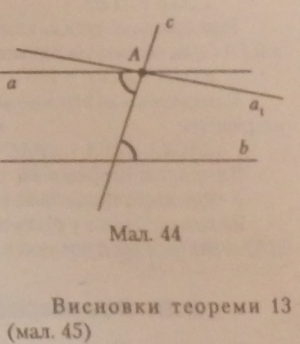
Теорема 13 (обернена до теореми 12) (властивість кутів, утворе - них при перетині паралельних прямих січною). Якщо дві паралельні прямі перетнуті третьою прямою, то внутрішні різносторошгі кути рівні» а сума внутрішніх односторонніх кутів дорівнює 180*.

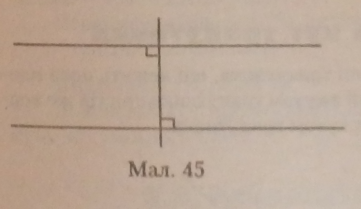
Якщо пряма перпендику* лярна до однієї з паралельних прямих, то вона перпендикулярна й до іншої прямої.

Дано три прямі а, Ь, с. Пряма с

— січна, а||6.

Довести, що внутрішні різно-сторонні кути рівні і сума внутрішніх односторонніх кутів дорівнює 180*

(мал. 44).

Доведення. Проведемо через точку А додаткову пряму а, так, щоб внутрішні різносторонні кути були рівні. Пряма а, збіжиться з прямою а за висновком задачі 1.