2. Відрізок. Вимірювання та відкладання відрізків. Відстань між двома точками

(2 год, уроки № 3, 4)

КОМЕНТАР ДЛЯ ВЧИТЕЛЯ

У результаті вивчення § 2 учні мають: знати: зміст понять відрізка, рівних відрізків, середини відрізка та довжини відрізка, зміст аксіоми вимірювання відрізків; зміст аксіоми відкладання відрізків та сфери її застосування; зміст поняття відстані між двома точками та властивостей рівних відрізків і властивостей порівняння відрізків;

уміти: розпізнавати на готовому рисунку відрізки (користуючись означенням) та за готовими рисунками робити записи, що відповідають аксіомі вимірювання відрізків, і навпаки; розв'язувати найпростіші задачі на застосування аксіоми вимірювання відрізків разом із вивченою раніше аксіомою розміщення точок на прямій; відтворювати аксіому відкладання відрізків; застосовувати названу аксіому для розв'язування відповідних задач; застосовувати властивості порівняння відрізків разом з аксіомою вимірювання відрізків для розв'язування задач на встановлення взаємного розміщення точок на прямій.

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ВИВЧЕННЯ МАТЕРІАЛУ

1. Означення відрізка, його елементи та позначення. Означення рівних відрізків. Середина відрізка. Довжина як міра відрізка. Одиниці вимірювання відрізків.

Насправді з навчальним матеріалом, викладеним у п. 2.12.3, учні знайомі ще з 5 класу. Тому основне завдання вчителя полягає в тому, щоб викласти цей, знайомий учням, матеріал із достатнім рівнем строгості, з посиланням на вивчений раніше теоретичний матеріал (аксіому розміщення точок на прямій). Висновки, отримані в ході вивчення матеріалу, учитель демонструє у вигляді таблиці «Відрізки». Уявлення про можливість суміщення або несуміщення відрізків бажано надати за допомогою наочної демонстрації (із використанням прозорої плівки) відповідно до опису, поданого в підручнику.

2. Аксіома відкладання відрізків.

Для мотивації вивчення аксіоми відкладання відрізків можна запропонувати учням таку задачу.

Задача. На промені OA відкладено відрізки OA = 8 см і OB = 1,2 дм. Яка з точок O, A, B лежить між двома іншими?

Таблиця

Відрізки

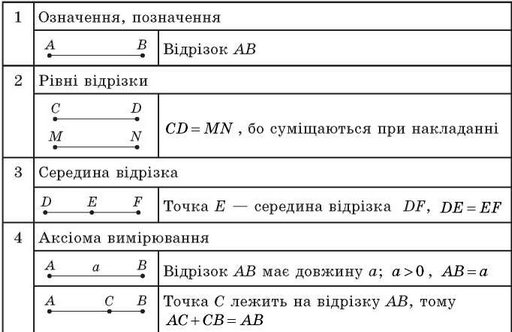
Після розв’язування запропонованої вчителем задачі цілком логічним є формулювання відповідної аксіоми (відкладання відрізків). Тепер стає зрозумілим питання застосування цієї аксіоми: для обґрунтування порівняння відрізків (як відкладання відрізків від початкової точки одного й того самого променя) без необхідності суміщати відрізки.

Говорячи про практичне застосування геометричних відомостей, логічно ввести поняття відстані між двома точками як довжини відрізка з кінцями у двох даних точках.

Розв’язання задачі, наведене на с. 17 підручника, також є важливим елементом навчального матеріалу, бо є зразком застосування поданих у § 1, 2 аксіом для обґрунтування міркувань.

МЕТОДИЧНІ КОМЕНТАРІ АВТОРІВ ПІДРУЧНИКА

Поняття «відрізок», «довжина відрізка», «середина відрізка» добре знайомі учням ще з початкової школи, тому завдання вчителя — звернути увагу на необхідність систематизації наявних знань, надання їм певної наукової строгості. Звертаємо увагу на те, що в нашому підручнику кінці відрізка є точками цього відрізка. Таке означення, по-перше, дозволяє уникнути непорозумінь щодо перетину відрізка з прямою, яка проходить

через один з його кінців, а по-друге, узгоджує геометричне означення відрізка з означенням числового відрізка (проміжку) в курсі алгебри.

Вводячи поняття рівності відрізків, слід звернути увагу на те, що означення рівності геометричних фігур через накладання є основним у даному підручнику. Поняття накладання інтуїтивно зрозуміле учням і може вводитися за допомогою моделей (накладання відрізків, накреслених на прозорій плівці, перегин паперового аркуша для визначення середини відрізка). Так само через накладання вводимо і порівняння відрізків.

Під час введення поняття довжини відрізка особливо слід виділити такі моменти:

1) довжина є кількісною характеристикою (мірою) відрізка (провести аналогію з мірами ваги, часу тощо);

2) введення поняття довжини відрізка спирається на відповідну аксіому;

3) існує прямий зв’язок між вимірюванням та накладанням відрізків — завдяки цьому порівняння відрізків через накладання узгоджується з порівнянням їх довжин;

4) через довжину відрізка визначається відстань між двома точками, а аксіоми проведення прямої та відкладання відрізків гарантують однозначність (коректність) такого визначення.

Розв’язуючи задачі цього параграфа, особливе місце відводимо відпрацюванню фактів, які очевидно випливають із вивчених аксіом та означень, але явно не сформульовані в тексті підручника (наприклад, такого: «Три точки однієї прямої визначають три відрізки, причому найбільший із них дорівнює сумі двох інших»).

ПЛАНУВАННЯ ВИВЧЕННЯ МАТЕРІАЛУ

На вивчення матеріалу § 2 відводиться два уроки.

На першому уроці:

у класі: вивчити означення відрізка, означення рівних відрізків та середини відрізка, зміст поняття довжини відрізка; розв’язати вправи:

усні вправи 1-4 (с. 22) (завдання 1 — на повторення матеріалу, вивченого на попередніх уроках);

[2]: № 39 графічно; № 41 (а), 43, 48 (а), 49 письмово; додаткову задачу (с. 23) письмово;

вдома: [2]: § 2, п. 2.1, 2.2, 2.3 (перша частина); контрольні запитання 6-9 на с. 56; розв’язати вправи:

[2]: № 32-34 усно; № 41 (б), 42, 44, 52 (а) письмово.

На другому уроці:

у класі: перевірити домашнє завдання, провівши математичний диктант (с. 23), вивчити зміст аксіоми відкладання відрізків; розібрати задачу, розв’язану в п. 2.3 підручника; розв’язати вправи: усні вправи 5-9 (с. 22-23);

[2]: № 45, 47, 51, 53, 55, 57, 59 письмово; вдома: [2]: § 2; п. 2.1-2.3; контрольні запитання 1-9 на с. 56; розв’язати вправи:

[2]: № 35-38 усно; № 31, 46, 52 (б), 56, 58 письмово; № 61 на повторення.

ВКАЗІВКИ ДО РОЗВ’ЯЗУВАННЯ ЗАДАЧ

1. Задачі на застосування аксіоми вимірювання відрізків.

Названий вид задач є першою спробою аргументованого (з посиланням на вивчені аксіоми) та алгоритмічного розв’язування геометричних задач на обчислення. Тому приклад розв’язання задач такого виду бажано записати в зошити учнів з відповідним коментарем.

Під час розв’язування задач потрібно вимагати від учнів міркувань, які приводять до застосування аксіоми вимірювання відрізків, а саме: якщо одна точка (А) з трьох точок (A, B, C) прямої лежить між двома іншими, то ця точка (А) належить відрізку з кінцями у двох інших точках (B і C), отже, виконується аксіома вимірювання відрізків (а саме: AC + AB = BC, тобто найбільший із трьох відрізків, що утворилися, дорівнює сумі двох інших). Тому далі, уже виходячи з умов задачі, або підставляємо відомі величини й виконуємо обчислення, або складаємо рівняння.

2. На другому уроці вперше розглядається задача, що передбачає два варіанти розв’язання залежно від взаємного розміщення точок на прямій, тому доцільно проаналізувати запропоноване в підручнику розв’язання цієї задачі ([2], с. 17).

3. Вправи № 45, 51 є вправами на закріплення способу дій, розглянутого у вищевказаній задачі; № 47, 53 — вправами, розв’язування яких передбачає комплексне застосування як аксіоми вимірювання відрізків, так і аксіоми відкладання відрізків разом із властивістю порівняння відрізків.

Усні вправи

(Рисунки заздалегідь підготовлено на дошці.)

1. Чи є правильними подані твердження?

а) Через точку площини можна провести не менше від 1000 прямих.

б) Маючи три точки площини, завжди можемо провести три різні прямі.

в) На кожній прямій можна позначити принаймні 1000 точок.

г) Із трьох точок на прямій принаймні одна лежить між двома іншими.

д) Дві різні прямі на площині можуть мати хоча б одну спільну точку.

2. За рис. 1, 2 опишіть взаємне розміщення точок і дайте відповіді на запитання.

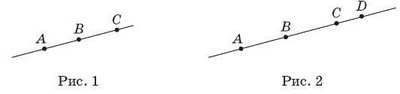
а) Скільки відрізків утворилось на рисунку?

б) Який з утворених відрізків найбільший? Чому?

3. Користуючись рис. 3, розв’яжіть задачі.

а) Дано: AB = CD. Доведіть, що AC = BD .

б) Дано: AC = BD . Доведіть, що AB = CD.

4. Чи дійсно AC = BC + AB (рис. 4)?

А Так Б Ні В Встановити неможливо

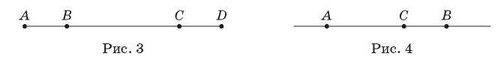
5. Відомо, що MN = MK + KN . Який з варіантів а-в на рис. 5 відповідає цій умові?

6. Скільки відрізків заданої довжини можна відкласти на даному промені від його початкової точки?

7. Скільки відрізків заданої довжини можна відкласти на даній прямій від даної точки?

8. Точки A, B і C лежать на промені AM, AB > AC. Чи може точка C лежати між точками A і B? Чи може точка A лежати між точками B і C?

9. Точки A, B і C лежать на одній прямій, AB > AC. Чи може точка C лежати між точками A і B? Чи може точка A лежати між точками B і C?

Математичний диктант

Зауваження: тут і далі дані, наведені у квадратних дужках,

призначені для другого варіанту.

1. Точка C лежить на відрізку AB. Нехай AC = 4 [7] см, AB = 9 [10] см. Яка довжина відрізка BC?

2. Чи може довжина відрізка виражатися дробовим додатним [цілим від’ємним] числом?

3. Чи може довжина відрізка дорівнювати нулю [числу 0,0001]?

4. Позначте точки M, P і K так, щоб справджувалася рівність MK + PK = MP [P + KP = MK].

Додаткова задача

На прямій позначено точки A, B, C так, що AB = 17 см, AC = 11 см, BC = 6 см. Яка з цих точок лежить між двома іншими? Чи зміниться відповідь, якщо AB = 17 см, AC = 11 см, BC = 28 см?

Це матеріал з посібника Розробки уроків з Геометрії за 7 клас Пабенко