Основні властивості рівнянь, ров'язування рівносильних рівнянь, лінійних рівнянь
Розв'язування рівнянь
|
Рівність — це два числа або два вирази, записані через знак рівності (рівні результати при обчисленні виразів зліва і справа від знака рівності). Приклади числових рівнянь: |
 |
|
Означення. Рівняння — це рівність, що містить невідоме (букву), значення якого поірібно знайти. |
Числову рівність 6-1-5 замінимо на буквену, прийнявши, що 6 • а. Одержимо рівність з одним невідомим: а -1 = 5.
Якщо в цю рівність підставити замість букви інші числа, крім 6, то після обчислень одержимо нерівності.
Наприклад, нехай а - 3 або а - 5, тоді:
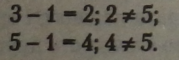
Отже, тільки в-6 — розв'язок нашого рівняння, або його корінь. Значення невідомого, при якому дане рівняння перетворюється на правильну рівність, називається коренем, або розв’язком даного рівняння*
Означення. Розв’язати рівняння — це означає знайти всі його корені або показати, що дане рівняння коренів иёмає.
Розв’язування рівняння (порядок знаходження кореня рівняння) залежить відтипу рівняння.
Типрівняння, у свою чергу, залежить від степеня невідомого (букви;-
— невідоме в першому степені — лінійне рівняння;
— невідоме в другому степені — квадратне рівняння;
• —невідоме в третьому степені — кубічне рівняння;
— невідоме в четвертому степені — рівняння четвертого степеня і т. д
Основні властивості рівнянь
1. У будь-якій частині рівняння можна розкривати дужки або зводити подібні.
2. Будь-який член рівняння можна переносити з однієї частини рівняння до іншої, помінявши його знак на протилежний.
3. Обидві частини рівняння можна помножити або поділити на одне й те саме число, крім нуля.
Обидві властивості рівнянь використовуються для утворення рівносильних рівнянь і для їх розв’язання (зведення до одного тотожного рівняння).
2.2. Розв'язування рівносильних рівнянь
Означення. Рівносильні рівняння — це два рівняння, які однаково розв'язуються (однаковий корінь).
Рівняння, які не мають розв'язків, також називаються рівносильними.
|
Приклади. |
 |
Порядок розв’язування рівносильних рівнянь
1. Замінити один вираз другим, йому тотожним, використовуючи другу з основних властивостей рівнянь.
Перенести числові вирази в одну частину рівності (за знак рівності), а буквені — в іншу.
2. Звести подібні члени (перша основна властивість рівнянь).
3. Розділити числовий вираз або число на коефіцієнт при невідомому, використовуючи третю основну властивість рівнянь.
Розв’язування рівносильних рівнянь застосовується до розв’язування дробових раціональних рівнянь.
Пр а в и л о. Щоб розв’язати дробове раціональне рівняння, його
треба звести до рівносильного цілого рівняння. Джя зведення
дробового рівняння до цілого треба знайти спільний знаменник дробів, додаткові множники до кожного члена рівняння, помножити чисельники дробів і цілі вирази на їх додаткові множники добутки взяти за доданки, а спільний знаменник відкинути.
2.3. Розв'язування лінійних рівнянь
Лінійні рівняння — це рівняння, у яких невідоме або невідомі є в першому степені. Лінійні рівняння бувають з одним невідомим, з двома чи більше невідомими. Розглянемо лінійні рівняння з одним невідомим.
Означення. Лінійне рівняння з однією змінною — це рівняння типу ахт Ь, де в і 6 — певні числа, постійні для цього рівняння, а х — змінна величина.
Розв’язування цього рівняння зводиться до знаходження числового значення невідомого х, що перетворює рівняння на рівність. Таке числове значення невідомого х називається коренем лінійного рівняння.
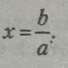
Корінь рівняння загального вигляду:
Оскільки aib — деякі раціональні числа, то при знаходженні х треба враховувати їх знаки для правильного обчислення знака в частці.
Будь-яке лінійне рівняння з однією змінною можна звести до загального вигляду, отже, і обчислити корінь рівняння.
|
Приклади. |
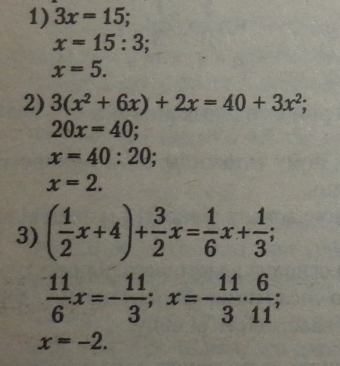 |
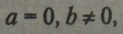
тобто вихідне рівняння
Рівняння не має коренів, якщо
набуває вигляду 0 • х - Ь.
Якщо а - 0 і b - 0, то рівняння має безліч коренів, оскільки рівність О-х-О правильна при будь-якому значенні X.

Автор: admin от 8-06-2013, 22:07, Переглядів: 13823