Тема 5. Рух тіла кинутого вертикально вгору (2 блок)

Розв'язання задач на рух тіла, кинутого під кутом до горизонту проводять за таким алгоритмом.

1 етап. Вибрати систему відліку, визначивши додатній напрям осей координат, початок відліку положення тіла і початок відліку часу. Якщо необхідно - зробити малюнок.

2 етап. Визначити за малюнком початкові умови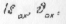 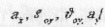і записати рівняння руху в проекціях на осі координат:

а) горизонтальному напрямі ОХ

б) вертикальному напрямі OY

3 етап. Використовуючи рівняння (1-4), знаходять невідомі величини.

4 етап. Проаналізувавши одержаний результат, і переконавшись в тому, шо знайдена величина мас фізичний зміст, запишіть відповідь.

Ми тут розглянемо найбільш загальний випадок руху тіла, кинутого під кутом до горизонту, оскільки рух тіла, кинутого вертикально вгору і горизонтально с частинним випадком розглядуваного руху.

Задача. З башти висотою 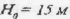кинули камінь у швидкістю 20 м/с під кутом а = ЗО^о до горизонту.

Знайти:

1) через який час тіло впаде на землю;

2) скільки часу піднімається тіло;

3) на якій відпалі від основи башти тіло впаде на землю;

4) на яку максимальну висоту піднімаються тіло;

5) знайти величину і напрям швидкості в точці падіння;

6) побудувати графік залежності висоти і далекості польоту, горизонтальної і вертикальної складових швидкостей та прискорення від часу. Опором повітря знехтувати.

Розв’язання.

1 етап.

Оскільки рух тіла відбувається в площині, то вибиремо прямокутну систему координат. Початок відліку суміщаємо з точкою земної поверхні (мал. 17).

2 етап.

Складний рух замінимо на 2 рухи

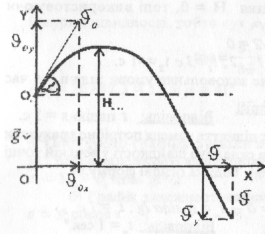
Перший з них відбувається у горизонталъному напрямі і є рівномірним, бо в горизонтальному напрямі ніякі сили не діють. Другий рух проходить у вертикальному напрямі і при піднятті с рівносповільненим, а при опусканні рівноноприскореним рухом, бо на тіло діє сила тяжіння, яка і зумовлює прискорення тіла. Швидкість тіла яка направлена під кутом а до горизонту, розкладемо на вертикальну і горизонтальну складові. Отже, задача зводиться до розглядання двох незалежних рухів вздож координат ОХ і ОУ.

Зафіксуємо початкові умови в горизонтальному і вертикальному напрямі і складемо рівняння руху.

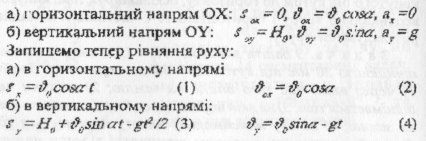
З етап.

Використовуючи рівняння руху (1-4) знаходимо невідомі величини.

1) Час падіння каменя можна знайти з умови, шо в точці падіння Н = 0, тоді використовуючи рівняння (3), маємо:

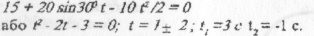
Оскільки час t₂= -1 не задовольняє умови задачі, то час падіння t = 3с.

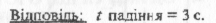
2. Щоб обчислити час підняття каменя потрібно врахувати той факт, що вертикальна складова швидкості у верхній точці траєкторії дорівнює нулеві. Тоді на основі формули

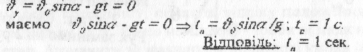
З. Знаючи час польоту t_пол = Зс можна обчислити далекість польоту каменя:

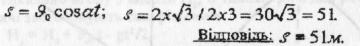
4. Максимальна висота підняття тіла над землею може бути обчислена за формулою

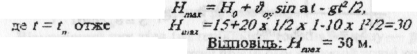
Можна максимальну висоту підняття знайти іншим способом:

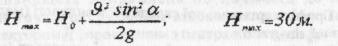
5) Величину швидкості руху тіла визначасмо за малюнком:

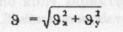
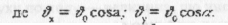
Отже, швидкість V_x направлена вертикально вниз, як і показано на малюнку.

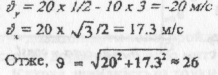
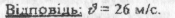
Напрям швидкості, тобто кут 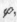знайдемо за малюнком

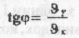
6. Побудуємо графіки функцій виду:

а) Графік залежності висоти від часу (мал.8)

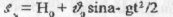
б) Графік залежності далекості польоту (мал.9)

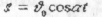
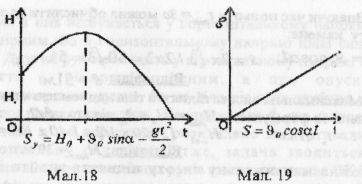
в) Графік вертикальної складової швидкості (мал. 20)

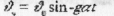
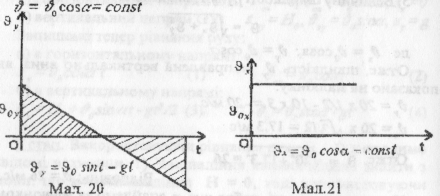
г) Графік горизонтальної складової швидкості. (мал.21)

Розв'язані задачі включають цілу серію простих задач, які розв’язуються аналогічно за одним і тим же алгоритмом.

1). Якщо H₀=0, то це випадок, коли тіло кидають під кутом до горизонту з початковою швидкістю V₀ з поверхні Землі. В такому разі рівняння (3) дещо спроститься:

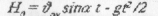
Решта рівнянь (1,2, 4) - аналогічні.

2). Якщо то задачі на рух тіла, кинутого горизонтально. Тоді рівняння в горизонтальному напрямі:

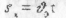
у вертикальному напрямі:

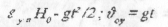
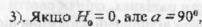то задачі на рух тіла, кинутого вертикально вгору з висоти Н₀, В такому разі для розв’язання задачі застосовують такі рівняння:

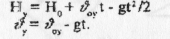
Рівномірний рух по колу.

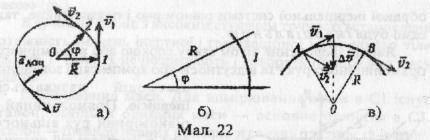
Рівномірний рух тіла (матеріальної точки) по колу — рух зі сталою за модулем швидкістю; при цьому в кожній точці кола миттєва швидкість напрямлена по дотичній до кола. Положення точки, шо рухається вздовж кола, визначається радіусом-вектором Л ♦ проведеним з центра кола до даної точки (мал.22 а).

Рівномірний рух по колу характеризується лінійною і кетового швидкістями. Лінійна швидкість під час рівномірного руху по колу — величина, що чисєльио дорівнює шляху, який проходить точка за одиницю часу;

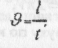
де l - довжина дуги кола, пройдена за час t. Лінійна швидкість чисельно дорівнює модулю миттєвої швидкості. Кутова швидкістьсо гочки, що рівномірно рухається коловою траєкторією, чисельно дорівнює відношенню кута 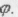на явзій повертається її радіус-вектор, до часу руху t:

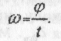
У фізиці прийнято вимірювати кути в радіанах (рад), а кутову швидкість — у радіанах за секунду (рад/с = 1/с = с^-1). Нагадаємо, що радіан — це безрозмірна одиниця виміру кута. Кут в 1 рад — це центральний кут між двома радіусами кола, довжина дуги між якими дорівнює радіусу. 1 рад ~ 57° 18'. Кут в радіанах і цей самий кут в градусах пов'язані співвідношенням:

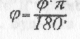
Щоб знайти значення кута φ в радіанах, слід провести з його вершини довільну дугу і знайти відношення довжини цієї дуги до радіуса R кола (мал.22б):

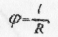
Зв’язок між лінією 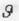та кутовою 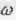швидкостями виражається формулою:

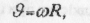
де R - радіус кола.

Період обертання Т — час одного повного оберту радіуса-вектора матеріальної точки, що рухається по колу. Частота обертання V показує, скільки обертів по колу здійснює тіло (точка) за одиницю часу. Частота, період та кутова швидкість пов’язані формулами:

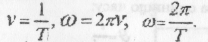
Під час рівномірного руху по колу модуль швидкості 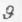має стале значення, а напрям вектора швидкості змінюється з часом. Вектор зміни швидкості

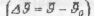
завжди спрямований до центра кола (мал.22 в). Тому рівномірний рух по колу — це рух з прискоренням:

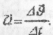
Прискорення, що характеризує швидкість зміни вектора миттєвої швидкості матеріальної точки під час її руху по колу, називається доцентровим прискоренням і позначається а_доц.Модуль доцентрового прискорення дорівнює:

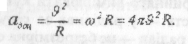
Напрям вектора змінюється з часом. У будь-якій точці кола вектор доцентрового прискорення напрямлений до центра кола, тобто перпендикулярно до вектора миттєвої швидкості.

Це матеріал із довідника "Фізика 9 клас"