Цілі вирази. Вирази зі змінними
Числовий вираз — це число або кілька чисел, сполучених знаком арифметичних дій.
Означення. Буквений вираз — це записи, складені з букв,
чисел і сполучені знаками арифметичних дій.
Якщо коефіцієнт виразу дорівнює 1, то він не пишеться, а перед буквеним виразом ставиться знак «+».
Якщо коефіцієнт виразу дорівнює -1, то він не пишеться, а перед буквеним виразом ставиться знак «-».
Приклади.
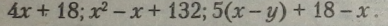
Означення. Степінь буквеного виразу визначається найбільшим степенем букв, що до нього входять.
|
Приклади. |
 |
Значення числового виразу можна одержати, виконавши всі за; дані дії.
Значення буквеного виразу можна обчислити, підставивши числові значення букв і виконавши вказані дії.
Якщо є кілька варіантів значень змінних, користуються табличною формою запрсу. Це робить результати наочними.
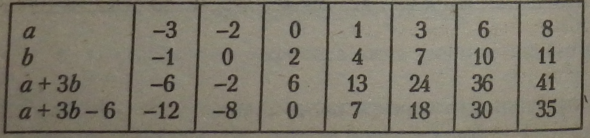
Приклад. Обчислити значення виразу (а + ЗЬ - 6) при заданих значеннях пар (а і Ь) букв, склавши таблицю для обчислення.
Правило. Змінна, яка стоїть у знаменнику дробу чи в дільнику » не може мати значення «О», оскільки вираз втрачає зміст.
Обчислення виразу
Правило. Щоб визначити значення буквеного виразу, треба:
1) спростити вираз (розкрити дужки, звести подібні);
2) підставити замість букв їх значення;
3) обчислити числове значення виразу.
При обчисленні виразів дійсні всі раніше вивчені закони додавання і множення (переставний, сполучний і розподільний).
Означення. Тотожно рівними називаються вирази, числові значення яких дорівнюють один одному при будь-яких значеннях букв, що до них входять.
Тотожне перетворення — це заміна одного виразу другим, тотожно рівним йому.
Тотожні перетворення виразів виконуються в основному з метою їх спрощення. При цьому застосовуються звичайні закони арифметичних дій.
Приклади.
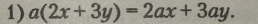
|
Перетворимо ліву частину: |
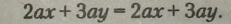 |
Ліва частина рівності дорівнює правій її частині, отже, заданий вираз є тотожністю.
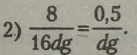
Рівність має зміст тільки при 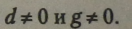
Перетворимо ліву частину рівності, скоротивши чисельник і знаменник дробу на 16:
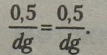
Оскільки одержали вірну тотожність, то задана рівність є тотожністю
Автор: admin от 7-06-2013, 23:50, Переглядів: 13878