§ 19. Рівняння руху. Графіки рівномірного прямолінійного руху

Рівняння руху. Рух тіла можна описати у різний спосіб. Наприклад, рух автомобіля можна описати так. Виїхавши з пункту А, автомобіль 3 год рухався рівномірно зі швидкістю 70 км/год. У пункті В водій зробив зупинку на 1 год і далі до пункту С їхав 2 год зі швидкістю 100 км/год.

За таким словесним описом руху можна визначити, що відстань між пунктами А і В становила 210 км, а між пунктами В і С — 200 км. Усього від пункту А до пункту С автомобіль подолав 410 км. Подорож тривала 6 год. Знаючи, де знаходиться пункт А і якою дорогою (траєкторію) рухався автомобіль, за картою автомобільних доріг можна з’ясувати, де саме розташовані відповідні пункти.

У фізиці для вивчення різних явищ широко використовують їх математичні моделі — рівняння руху. Рівняння руху дають змогу лаконічніше описати увесь процес руху та виділити його особливості. Такі рівняння показують, як залежать швидкість, шлях, переміщення, координата тіла (характеристики руху) від часу. Відповідно рух певного тіла можна описати рівняннями швидкості, рівняннями пройденого шляху, рівняннями координати та ін.

Опис руху розглядуваного автомобіля за допомогою рівнянь швидкості і шляху матиме такий вигляд:

Ці рівняння відображають залежність швидкості і пройденого автомобілем шляху від часу. За рівняннями швидкості можна зробити висновок: на усіх ділянках шляху швидкість не залежала від часу. Рух був рівномірним. Відлік часу починається з моменту виїзду автомобіля з пункту А. Скориставшись цими рівняннями, можна визначити шлях, подоланий автомобілем за будь-який час протягом перебування в дорозі, особливості його руху, швидкість, з якою він рухався протягом того чи іншого проміжку часу.

Якщо окремо не зазначено одиниці вимірювання часу, шляху, швидкості, то вважають, що ці величини визначено в одиницях СІ. Наприклад, рівняння шляху автомобіля має вигляд: s = 10С Це означає, що швидкість автомобіля становить

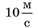
тоді час слід визначати в секундах, а шлях — у метрах

(табл. 1.1).

Таблиця 1.1. Залежність пройденого шляху від часу

Таблиця дає інформацію про особливості руху автомобіля. З її аналізу можна дійти висновку, що, наприклад, після трьох годин руху, подолавши 210 км, водій годину відпочивав. Потім протягом двох годин він рухався, долаючи щогодини 100 км.

Графік пройденого шляху. Залежність між величинами, які характеризують рух, можна відобразити і за допомогою графіка. Незалежною змінною величиною, тобто такою, на зміну якої не впливають інші величини, ми вважаємо час. Принаймні плин часу не залежить від того, рухається автомобіль чи стоїть на місці. Та й ви, залежно від того, чи їхали до школи автобусом, чи йшли пішки, не помічали, що ваш годинник відстав. У математиці такі величини називають аргументами. їх значення прийнято відкладати уздовж горизонтальної координатної осі— осі абсцис або осі X. Залежні від них величини відкладають уздовж осі ординат — вертикальної осі, яку позначають Y.

Фізики мають справу з багатьма величинами. У кожної з них є власна назва й позначення. Тому на графіках, що відображають залежності між фізичними величинами, осі позначають відповідно до позначень цих величин. Значення незалежної змінної величини (часу) прийнято відкладати уздовж осі абсцис, а значення величин, які можуть із часом змінюватися (шлях, швидкість, координати й інші), — уздовж осі ординат.

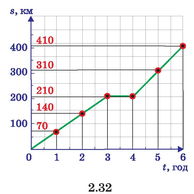
Графік, що відбиває залежність шляху, пройденого автомобілем, зображено на мал. 2.32. Його називають графіком шля

ху. За графіком шляху легко з’ясувати, що за 2 год після виїзду з пункту А автомобіль проїхав 140 км. Через 3 год, подолавши 210 км, він зупинився і протягом однієї години стояв (шлях не змінювався). Через 6 год він досяг кінцевого пункту, проїхавши 410 км. За графіком можна легко визначити й швидкості, з якими рухався автомобіль. Наприклад, якщо за дві години свого руху він проїхав 140 км, то його швидкість становила

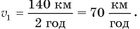
З третьої до четвертої години (час зупинки) його швидкість дорівнювала нулю. Після зупинки, проїхавши 200 км за 2 год,

він рухався із швидкістю

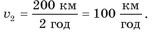
Зверніть увагу!

За більшої швидкості руху лінія графіка шляху утворює з віссю часу більший кут.

Графік швидкості. Використовуючи графік, можна описати, як із часом змінювалася швидкість тіла. Графік, що відображає залежність швидкості руху тіла від часу, називають графіком швидкості. Графік швидкості руху автомобіля, про який йшлося вище, показано на мал. 2.33. Під час рівномірного руху швидкість не змінюється. Такий рух автомобіля відображають ділянки графіка ab та ef. Усі точки відрізка ab мають ординату км

70    , що відповідає швид-

год

кості автомобіля протягом трьох годин на шляху від пунк-

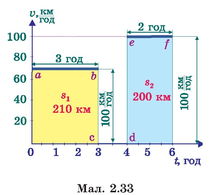
ту А до пункту В, тобто до зупинки. У пункті В автомобіль стояв. Протягом однієї години його швидкість дорівнювала 0. Цей стан автомобіля відбиває ділянка графіка cd. Нарешті, ділянка графіка ef відображує рух автомобіля із сталою швидкістю 100 км/год протягом наступних двох годин.

За графіком швидкості легко визначити пройдений автомобілем шлях. Пригадайте, щоб знайти шлях, пройдений тілом під час рівномірного руху, необхідно швидкість тіла помножити на час руху. З графіка видно, що добуток швидкості на час руху автомобіля з цією швидкістю при рівномірному русі чисельно дорівнює площі прямокутника, обмеженого відповідним відрізком графіка швидкості (добутку його сторін):

Розглянуті нами графіки шляху і швидкості описують лише окремий, ідеальний випадок руху. Насправді жоден автомобіль не може увесь час рухатися рівномірно. Графіки, що відображають реальні рухи, можуть бути значно складнішими. Загалом їх називають графіками руху. За графіками руху можна визначити пройдений тілом шлях, його координату у певний момент часу (тобто місце розташування), швидкість та інші характеристики. Треба тільки розуміти мову графіків і вміти їх “читати”.

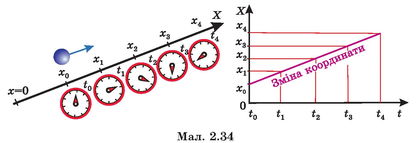
Графік координати. Нехай тіло рухається по прямій, уздовж якої ми спрямуємо також вісь координат X. Під час руху тіла його координата х змінюватиметься. Наприклад, у початковий момент часу t₀ = 0 тіло перебуває у положенні х₀ (х₀ називають початковою координатою), а в моменти часу t₁, t₂, t₃, t₄ — у точках з координатами х₁, х₂, х₃, x₄. Відклавши на горизонтальній осі (абсцис) час, на вертикальній (ординат) — координату, отримаємо графік залежності координати від часу: x(t) (x(t) читається як “ікс від те” і означає, що величина х змінюється залежно від значення t (мал. 2.34)).

Графік координати дає змогу визначати положення (координату) тіла у той чи інший момент часу:

•    з якої точки воно починало рух (початкову координату);

•    в якій точці тіло припинило рух (кінцеву координату);

•    де тіло перебувало в той чи інший момент часу t (поточну координату).

Нехай за проміжок часу t тіло перемістилося в точку з координатою х. Тоді координату тіла на той чи інший момент часу можна знайти, відклавши уздовж координатної осі від початкової координати довжину вектора переміщення s (або пройдений за цей час шлях): х = х₀ + s. Урахувавши, що s = = vt, можна записати: х = х₀ + vt. Ми одержали рівняння координати, яке показує, як залежить координата від часу.

Наприклад, рівняння координати, що має вигляд х = 20 + + 10t, математично описує таку можливу ситуацію. Пройшовши на зупинку автобуса, ви побачили, що він від’їхав від зупинки на 20 метрів (початкова координата) і продовжує рухатися зі швидкістю

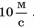
Ще один приклад. Велосипедист почав свій рух від дорожнього знака (початкова координата х₀ = 150 м), через 30 с його координата х₁ = 300 м, а в момент часу t₂ = 50 с він перебуває в точці з координатою х₂ = 400 м (мал. 2.35).

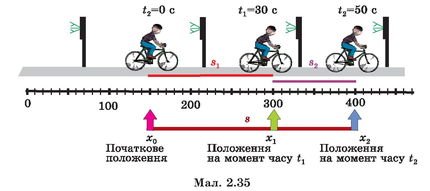
Запишемо рівняння координати велосипедиста. Початкова координата відома (х₀ = 150 м). Щоб знайти швидкість, потрібно знати шлях і час, за який він пройдений. Шлях можна обчислити за різницею координат. Так, за перші 30 с велосипедист, зображений на малюнку, проїхав шлях s₁= \x₁ — x₀|, або s₁ = 300 м — 150 м = 150 м. Отже, швидкість його рівномірного руху становить

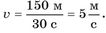
Рівняння руху велосипедис

та матиме вигляд x =150+ 5t.

Повний шлях за увесь час руху й_повн = \х₂ — x₀\ = 400 м — — 150 м = 250 м. Різниця координат береться за модулем, оскільки тіло може рухатися не тільки в напрямку осі координат, а й протилежно до нього. Тоді різниця координат буде від’ємною, а шлях — завжди додатним. Шлях s₂, пройдений від моменту часу t₁ до моменту t₂, визначається так: s₂ = \х₂ — x₁\ = = 400 м — 300 м = 100 м (див. мал. 2.35).

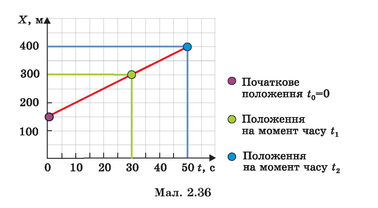
Графік координати, що відповідає такому руху велосипедиста, матиме вигляд, як на мал. 2.36.

Зверніть увагу!.

1.    Лінія графіка координати починається не в нулі, а у значенні х = х₀ = 150 м.

2.    Під час руху в напрямку осі X координата зростає й лінія графіка піднімається.

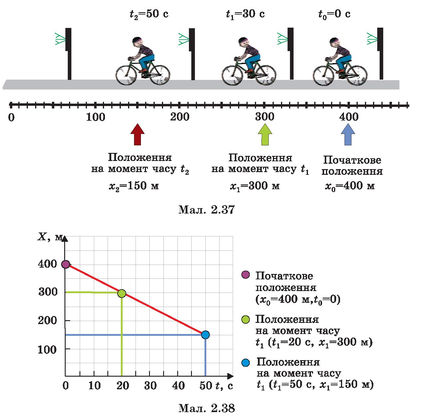
Якщо велосипедист рухається в напрямку, протилежному до напрямку осі X (мал. 2.37), то координата із часом зменшуватиметься й графік координати буде спрямований униз (мал. 2.38).

Придивіться уважно, за будь-які однакові проміжки часу, наприклад за кожні 10 с (мал. 2.36, 2.38), координата змінюється на 50 м. Тобто за будь-які рівні проміжки часу велосипедист долав однакові відстані — його рух був рівномірним. У випадку рівномірного руху графік координати є прямою, що починається в точці х₀ (у нашому випадку х₀ = 150 м для першого випадку й х₀ = 400 м, коли велосипедист рухався у протилежний бік до обраного напрямку осі координат).

На мал. 2.39 наведено графіки для двох тіл, що рухаються рівномірно, але з різними швидкостями. Тіло B рухається швидше, ніж тіло A: лінія, що відображає графік координат тіла А, є більш похилою, ніж лінія руху тіла B. Дійсно, якщо швидкість тіла більша, то воно швидше змінює своє положення й, відповідно, координати.

За допомогою графіка координати можна легко визначити швидкість тіла. Для цього слід обрати на графіку будь-які дві точки. Модуль різниці координат цих точок дорівнюватиме шляху, пройденому тілом, а різниця відповідних їм моментів часу — часу руху. Відношення \х₂ — xj/(t₂ — Ц) — це швидкість руху тіла.

Наприклад, для визначення швидкості тіла А оберемо точки графіка, що відповідають моментам часу 2 с і 4 с від початку відліку часу руху. їм відповідають координати х₁ = = 3 м та х₂ = 6 м. Пройдений тілом шлях дорівнюватиме s_A = X_A2 — x_A1 = 6м — 3м = 3 м. Цей шлях тіло пройшло за час t_A = t_A2 — t_A1 = 5с— 2 с = 3 с. Отже, швидкість тіла А становитиме

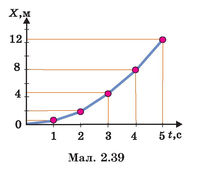
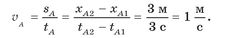
Для визначення швидкості тіла В зручніше обрати точки графіка, що відповідають моментам часу t_B1 = 1 c і t_B2 = 4 c та координатам х_В1 = 3 м, х_В2 =12 м. Виконавши відповідні обчислення, одержимо

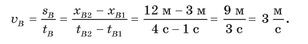
Якщо тіло не рухається, то його координата не змінюється й графік координати буде прямою, паралельною осі часу (мал. 2.40).

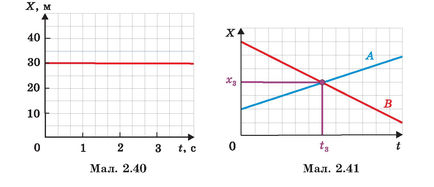
Якщо тіла рухаються назустріч одне одному або одне тіло наздоганяє інше, то в момент зустрічі їх координати однакові. Точка перетину графіків координат двох тіл визначає час і координату їхньої зустрічі (мал. 2.41).

ЗАПИТАННЯ ТА ЗАВДАННЯ

1.    Що являє собою графік шляху? Залежність між якими величинами, що характеризують рух, він відображає?

2.    На мал. 2.42 зображено графіки шляху трьох тіл. Швидкість якого тіла найбільша, а якого найменша?

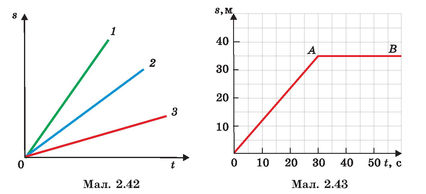
3.    За графіком шляху пішохода (мап. 2.43) визначити: а) як рухався пішохід протягом усього часу спостереження; б) шлях, пройдений ним за 30 с та за увесь час спостереження; в) швидкість, з якою рухався пішохід перші 30 с.

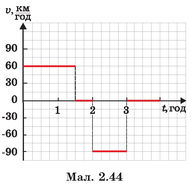
4.    На мап. 2.44 зображено графік швидкості автомобіля. За графіком визначити:

1)    з якою швидкістю рухався автомобіль протягом перших 1,5 год від початку руху;

2)    скільки часу рухався автомобіль;

3)    якою була швидкість автомобіля через 2,5 год після початку спостереження руху;

4)    який шлях проїхав автомобіль до першої зупинки;

5)    який шлях подолав автомобіль протягом усього часу спостереження;

6)    на якій відстані (де) відносно його положення на момент початку спостереження знаходився автомобіль з третьої до четвертої години спостереження за ним, якщо він увесь час рухався однією і тією самою дорогою.

За графіком швидкості побудуйте графік координати і графік шляху цього автомобіля.

Це матеріал з підручника Фізика 7 клас Бойко, Венгер, Мельничук.