Равномерное движение материальной точки по окружности. Период вращения
Более 5000 лет назад жрецы древнего Вавилона, наблюдая за Луной, определили такой хорошо известный нам интервал времени, как неделя. Как они это сделали? В чем особенность движения Луны? Встречается ли на Земле подобное движение? В данном параграфе вы найдете ответы на эти и многие другие вопросы.
Знакомимся с движением по окружности
Попробуйте представить линию, вдоль которой движутся ребенок, кружащийся на карусели, носок в барабане стиральной машины во время отжима, кончик ножа блендера при изготовлении коктейля или смузи. Уверены, что вы легко определили: этой линией является окружность. Итак, в перечисленных случаях имеем дело с движением по окружности; простейшим является равномерное движение по окружности. Далее, говоря о равномерном движении по окружности любого физического тела, будем считать это тело материальной точкой.
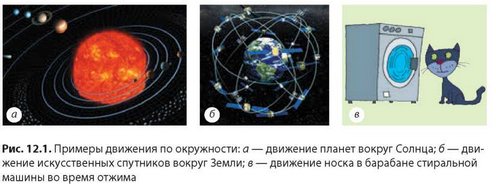
Равномерно по окружности движутся, например, кабинки колеса обозрения. Близким к равномерному движению по окружности является движение планет вокруг Солнца (рис. 12.1, а), естественного спутника (Луны) или искусственных спутников вокруг Земли* (рис. 12.1, б).
Приведите примеры движения по окружности. В каких случаях это движение можно считать равномерным? Можно ли считать движение точек обода колеса велосипеда относительно его рамы равномерным движением по окружности? Обоснуйте свой ответ.
Точнее — планеты и спутники движутся по эллиптическим орбитам.
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь.
Определяем период вращения
Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные равные интервалы времени. Например, кончик секундной стрелки часов, двигаясь равномерно вдоль циферблата, повторяет свое движение через каждые 60 с (рис. 12.2).
Любое периодическое движение характеризуется такими физическими величинами, как период и частота. При равномерном движении по окружности говорят о периоде вращения и частоте вращения.
Период вращения — это физическая величина, равная времени, за которое материальная точка, равномерно движущаяся по окружности, совершает один оборот.
Период вращения обозначают символом T.
Единица периода вращения в СИ — секунда:
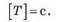
Период вращения равен одной секунде, если за одну секунду совершается один оборот.
Кончик секундной стрелки часов совершает один оборот за 60 с, поэтому период его вращения, как и каждой точки секундной стрелки, равен 60 с (( = 60 с).
Подумайте, каковы периоды вращения точек минутной и часовой стрелок часов. Когда взбивают молочный коктейль блендером, каждая точка его ножа за 30 с делает 6000 оборотов (рис. 12.3). Чтобы определить время одного оборота, нужно


Таким образом, чтобы определить период вращения Т, следует подсчитать количество оборотов N. совершенных за интервал времени t, и воспользоваться формулой:
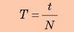
Определяем частоту вращения
Указывая технические характеристики устройств, используют не период вращения, а частоту вращения (рис. 12.4).
Частота вращения — это физическая величина, которая равна количеству оборотов за единицу времени.
Частоту вращения обозначают символом п и определяют по формуле:
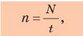
где t — время вращения; N — количество оборотов за данное время. Единица частоты вращения в СИ — оборот в секунду:
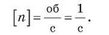
Учитывая, что
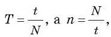
приходим к выводу, что период вращения и частота вращения являются взаимно обратными величинами:
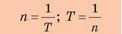
Чем больше период вращения тела, тем меньше его частота вращения, и наоборот.
I Попробуйте рассчитать частоту, с которой вращаются точки ножа блендера (см. рис. 12.3).

Узнаем, как возникли единицы времени: сутки и неделя
Как измерить время? Ответ на этот вопрос подсказала людям сама природа. Дело в том, что многие движения, происходящие в природе, являются периодическими, а период такого движения может служить единицей времени. Например, вращение Земли вокруг своей оси — периодическое движение. Ежедневный восход (закат) Солнца, обусловленный этим движением, подсказал нашим предкам единицу времени сутки, которые равны периоду вращения Земли вокруг своей оси.
Несколько единиц времени были получены в древнем Вавилоне. Наблюдая за ночным небом, жрецы заметили, что «молодая» Луна появляется на небосклоне приблизительно каждые 28 суток. Периодическое рождение лунного диска служило своего рода вечными «часами». Так возникла единица времени месяц*. За это время Луна, вращаясь вокруг Земли, проходит полный цикл изменения фаз: новолуние, первая четверть, полнолуние, последняя четверть (рис. 12.5). Именно поэтому жрецы разделили лунный месяц на четыре части (по количеству лунных фаз) и получили семь дней — единицу времени, которая называется неделя.
Определяем скорость равномерного движения по окружности
Кроме периода вращения и его частоты важной характеристикой движения по окружности является скорость движения. Если тело равномерно движется по окружности, то за время, равное периоду вращения (= Т , тело совершает один оборот, то есть проходит путь, равный длине окружности. Длину окружности l можно вычислить по известной вам из математики формуле: I = 2лИ, где л = 3,14 — математическая константа; К — радиус окружности.
Зная путь и время, за которое этот путь пройден, получаем формулу для расчета скорости равномерного движения по окружности:
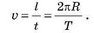
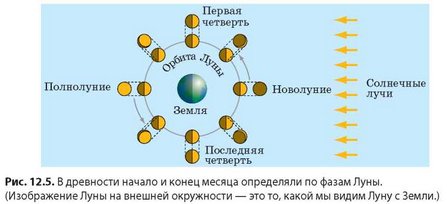
Сейчас, как правило, используют понятие календарного месяца, который не зависит от фаз Луны и длится от 28 до 31 суток.
Именно об этой скорости идет речь, когда, например, определяют скорость движения человека, кружащегося на карусели, говорят о скорости полета искусственных спутников Земли и т. д.
Подводим итоги
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь. Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные одинаковые интервалы времени.
Период вращения Т — физическая величина, равная времени, в течение которого материальная точка, равномерно движущаяся по окружности, совершает один оборот. Единица периода вращения в СИ — секунда (с).
Частота вращения п — это физическая величина, которая равна количеству оборотов за единицу времени. Единица частоты вращения в СИ — оборот в секунду (об/с, или 1/с).
Период вращения Т и частоту вращения п определяют по формулам:
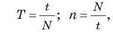
где t — время наблюдения; N — количество оборотов за это время. Частота вращения и период вращения — взаимно обратные величины:
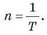
Контрольные вопросы
1. Какое движение называют равномерным движением по окружности?
2. Какое движение называют периодическим? Почему равномерное движение по окружности является периодическим? 3. Какие физические величины характеризуют периодическое движение? 4. Дайте определение периода вращения. 5. Как вычислить период вращения? 6. Дайте определение частоты вращения. 7. Как вычислить частоту вращения, если известен период вращения? 8. Наблюдение за каким процессом послужило причиной появления таких единиц времени, как месяц и неделя?
Упражнение № 12
1. За 18 секунд колесо автомобиля сделало 24 оборота. Определите период вращения точки на ободе колеса.
2. Какова частота вращения точек патрона электродрели, если за минуту патрон совершает 900 оборотов?
3. На лопасть отключенного вентилятора прикрепили маленькую наклейку со смайликом. С какой частотой будет вращаться смайлик, если лопасти вентилятора будут совершать один оборот за 0,2 с?
4. Известно, что вентилятор микропроцессора персонального компьютера вращается с частотой 3600 об/мин. Определите период вращения точек лопастей вентилятора.
5. Мальчик кружился на карусели 5 мин. За это время он совершил 100 оборотов. В каком случае можно утверждать, что период вращения мальчика был равен 3 с? Ответ обоснуйте.
6. Четыре шестерни скреплены зубцами так, как показано на рис. 1. Шестерня 1 имеет 9 зубцов, шестерня 2 — 15 зубцов, шестерня 3 — 8 зубцов, шестерня 4 — 16 зубцов. Шестерни 2 и 3 закреплены на общем валу. Определите период вращения шестерни 4, если частота вращения шестерни 1 равна 5 об/с.
■5€· 7. Скорость движения диска «болгарки» (рис. 2) в точке соприкосновения с обрабатываемой поверхностью должна быть не менее 80 м/с. Какими при такой скорости будут частота вращения и период вращения диска, если его диаметр равен 160 мм?
*8 . Воспользовавшись дополнительными источниками информации, сравните средние радиусы орбит планет — Венеры, Земли, Марса, а также периоды их вращения вокруг Солнца. Определите скорости движения этих планет относительно Солнца. Подготовьте презентацию.

Экспериментальное задание
«Вращение в быту». Вместе со взрослыми определите период вращения и частоту вращения стакана с жидкостью, подогреваемой в СВЧ-печи. Какие измерения вы осуществили, чтобы выполнить задание? ^ Определите скорость, с которой вращается стакан, стоящий на краю поворотного столика СВЧ-печи.
ЛАБОРАТОРНАЯ РАБОТА № 4
Тема. Измерение периода и частоты вращения.
Цель: измерить период и частоту вращения тела при его равномерном движении по окружности.
Оборудование: пластиковый шарик или другое небольшое тело (пуговица, ключ и т. п.), которое можно легко закрепить на нити; лист бумаги с изображением окружности радиусом 15 см; крепкая нерастяжимая нить длиной 50-60 см; секундомер; линейка.
УКАЗАНИЯ К РАБОТЕ Подготовка к эксперименту
1. Убедитесь, что вы знаете ответы на следующие вопросы.
1) Какое движение называют равномерным движением по окружности?
2) По какой формуле вычисляют период равномерного движения тела по окружности? По какой формуле вычисляют частоту вращения?
2. Прикрепите шарик (или другое небольшое тело) к нити. На свободном конце нити сделайте петлю, за которую вы будете держать нить, вращая тело в горизонтальной плоскости.
Эксперимент
Строго придерживайтесь инструкции по безопасности (см. форзац). Результаты измерений сразу заносите в таблицу.
1. Возьмите за петлю нить с телом. Расположите руку над центром изображенной окружности.
Не меняя положения руки, заставьте тело двигаться так, чтобы траектория его движения совпадала с окружностью.
2. Измерьте время t, за которое тело выполняет 10 оборотов; 15 оборотов.

Обработка результатов эксперимента
Определите период и частоту вращения тела при его равномерном движении по окружности. Результаты занесите в таблицу.
Анализ эксперимента и его результатов
Проанализировав эксперимент, сделайте вывод, в котором укажите: 1) какое движение вы изучали; 2) значение каких величин определяли;
3) какие результаты получили; 4) какие факторы влияли на точность результатов.
Творческое задание
В плохо освещенном помещении благодаря особенностям зрения человек может различать события как отдельные, если интервал времени между ними составляет более 0,2-0,3 с. С какой частотой нужно двигать по окружности «бенгальский огонь», чтобы увидеть светящееся кольцо?
Задание «со звездочкой»
Запишите результаты измерения периода вращения тела в виде:
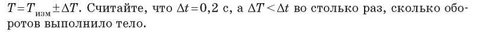
Это материал учебника Физика 7 класс Барьяхтар, Довгий
Автор: admin от 24-01-2017, 07:24, Переглядів: 4730