Розділ 1. Математичні основи обчислювальної техніки
Загальні відомості про системи числення; арифметичні операції в позиційних системах числення; перетворення чисел із одної системи числення в іншу; способи подання чисел у комп’ютерах.
1.1. Поняття про системи числення. Позиційні та непозиційні системи числення
Системою числення називається сукупність правил запису (зображення, подання) чисел за допомогою символів (цифр) і виконання операцій над ними.
Розрізняють непозиційні та позиційні системи числення.
У пепозиційних системах числения значення цифри не залежить від її місця розташування в зображенні числа. Такі системи досить складні для запису чисел і виконання над ними арифметичних дій. Нині використовується тільки римська система числення, в якій числа записуються за допомогою таких цифр: І (один), V (п’ять), X (десять), Ь (п’ятдесят), С (сто), Б (п’ятсот), М (тисяча).
Якщо кілька однакових цифр записано поряд, то їх значення додаються, наприклад, III (один + один + один = три), СС (двісті), XXX (тридцять). Якщо цифра, яка позначає менше число (молодша цифра), стоїть праворуч від цифри, яка позначає більше число (старшої), то її значення додасться до старшої, наприклад VII (сім), XIII (тринадцять). Якщо молодша цифра стоїть ліворуч від старшої, то вона віднімається від неї, наприклад, IX (десять відняти один = дев’ять), ХЬ (сорок).
У позиційних системах числення значення цифри залежить не тільки від самої цифри, але й від її місця (позиції) у записі чиеіа.
У звичній для нас десятковій системі числення числа записуються за допомогою цифр: 0,1,2,3,4,5,6,7,8,9, розташованих певним чипом.
Наприклад, у числі 64 значения цифри 6 дорівнює 60, а в числі 40,6 — 0,6 (шість десятих). Кожна позиція цифри називається розрядом. Для цілих чисел використовується така нумерація розрядів: молодший (із найменшими значеннями цифр) розряд цілого числа мас номер нуль,
а кожний наступний номер збільшується на одиницю. У дробовій частині, вираженій десятковим дробом, старший розряд мас номер —1, а кожний наступний номер зменшується на одиницю. Таким чином, якщо ціла частина числа має п розрядів, а дробова — т розрядів, то старший розряд цілої частини має номер <п-1>, а молодший розряд дробової частини — номер <-т>. У табл. 1.1 подано нумерацію розрядів для десяткового числа 71453,2649.
Таблиця 1.1

Основними характерист иками позиційних систем числення є: основа системи числення; вага розрядів; — значення цифр, які використовуються в системі числення.
Основою системи числення (з) називають кількість цифр, які можуть використовуватися в кожному розряді числа.
У десятковій системі числення застосовуються цифри 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Основа системи числення визначає її назву (десяткова, вісімкова, двійкова тощо).
Вагою розряду називають число, на яке треба помножити значення розміщеної у ньому цифри.
База розрядів у позиційних системах зазвичай приймається рівною основі системи числення у степені, що дорівнює номеру розряду.
Наприклад, у десятковому числі 725 вага другого розраду дорівнює 102= 100, а в числі 0,4563 вага розраду -3 дорівнює 1(Н = 0,001. Десяткова система числення є системою з природішм порядком ваги розрядів, тобто вага кожного настзчшого розряду більша, ніж вага попереднього розряду в кількість разів, що дорівнює основі системи числення, а у дробовій - менша у стільки ж разів.
Застосовуються й системи числення з вагою розрядів, відмінною від природної. Таку вагу розрядів називають штучною.
Перевіряємо себе
1. Що таке система числення?
2. Що називається основою системи числення?
3. Які системи числення називають позиційними?
4. Чим відрізняється цифра від числа?
5. Що називається розрядом числа?
Поясніть, чому вираз "цифра відмінників у класі, зоосла" та інші подібні є неправильними.
Назвіть основні ознаки позиційних систем числення.
8. Поясніть, як визначається вага розрядів у позиційних системах числення.
іу. Скільки цифр потрібно для подання чисел у вісімковій
системі числення?
10. Скільки цифр потрібно для подання чисел V двадцятковій системі числення?
Виконуємо
1. Запишіть позначки годин па циферблаті римськими цифрами. Зробіть це для годинника, годинна стрілка якого робить один оберт за добу.
2. Для числа 144(іо) визначте значення кожного розряду
Подайте числа 8<к», 32(ю), 64<ю), 128<и», 256(ю), 512(ю), 1024(іо) у двійковій системі числепня. Поясніть, у чому7 особливість цих чисел.
Запишіть дату, якої ви виконуєте це завдання, в форматі: місяць, число, рік римськими цифрами, у двійковій, вісімковій. десятковій, шістнадцятковій системах числення.
1.2. Системи числення, що використовуються в обчислювальній техніці
У обчислювальній техніці основною системою числення с двійкова систеліа зі символами Oil.
Крім двійкової застосовуються також десяткова, двійково-десяткова і шістпадцяткова системи числення.
Будь-який тип даних (текстовий, графічний, відео тощо) у комп'ютерних системах подається символами 0 і 1, бо подання й опрацювання даних здійснюється електронними пристроями, в яких електричні сигнали набувають лише двох значень (бістабільними пристроями). Ці значення позначаються символами Oil.
Наприклад, сигналу з напругою ЗВ відповідає значення 1, а сигналу* напругою 0В - 0. Такі пристрої дуже надійні, позаяк
встановлено однозначну відповідність між фізичними та математичними величинами.
Двійкова система числения порівняно з іншими системами найпростіше й надійніше реалізується технічно.
У двійковій системі числення найпростіше виконуються арифметичні операції.
Двійкова система має досить прості правила додавання:
0 + 0 = 0, 0 + 1=1, 1 + 0 = 1, 1 + 1 = (1) 0, (у дужках - одиниця, перенесена в старший розряд).
Таблиця множення двійкових чисел також проста:
00= 0, 0-1 = 0, 1-0= 0, 1-1= 1.
Простота виконання арифметичних операцій на папері означає, що й електронні схеми, які реалізують ці операції, також досить прості. Теоретично обґрунтовано, що двійкова система за апаратними витратами є однією з економних систем. За цим показником вона незначно поступається лише трійковій системі числення.
Електронні схеми з двома стійкими станами мають малий час переходу з одного стану в інший, і навпаки. Це означає, що в таких системах швидкість виконання арифметичних операцій висока.
Двійкова система (як і десяткова) є позиційною системою. Нагадаємо, що в таких системах кількісне значення цифри залежить як від значення цифри, так і від її розташування (позиції, розряду) в записі числа. З урахуванням номера розряду й основи системи числення визначається кількісний еквівалент кожної цифри.
Наприклад, у десятковому числі 326,75 цифра 3 розміщена в другому розряді й позначає число з 3-Ю2 = 300 одиниць, цифра 2 розміщена в першому розряді й позначає число з 2-Ю1 = 20 одиниць, цифра 6 розміщена в нульовому розряді й позначає число з 6 10° = 6 одиниць, цифра 7 розміщена в мінус першому розряді й позначає число з 7-Ю1 = 0,7 одиниць, цифра 5 розміщена в мінус другому розряді й має 5*Ю 2 = 0,05 одиниць. Подане десяткове число може бути записане у вигляді суми: 326,75 = 3-Ю2 + 210і + 610°+ 7-Ю1 + 5-102.
Для того щоб визначити кількісне значення цифри в позиційній системі числення., треба помножити цю цифру на основу системи в степені того номера розряду, в якому розміщена ця цифра.
Наприклад, двійкове число 1011.01 можна записати у вигляді
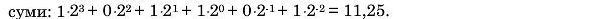
Таким чином, двійковий запис 1011,01 є десятковим числом 11,25. У табл. 1.2 наведені десяткові цифри, двійкове подання їх значень і двійковий запис чисел у вигляді сум.
Таблиця 1.2
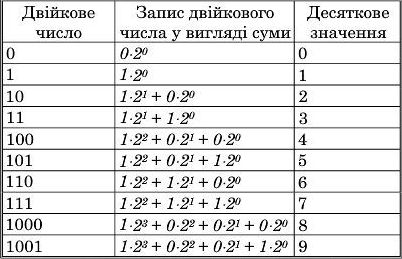
У комп'ютерах крім двійкової і десяткової систем числення використовуються також двійково-десяткова та шісиадцяткова системи числення. У двійково-десятковій системі числення кожний розряд десяткового подання подасться чотирма двійковими розрядами. Наприклад, десяткове число 618,74 має такий запис у двійково-десятковому поданні:
0110 0001 1000, 0111 0100 - двійково-десятковий запис,
6 18,74 — запис у десятковій системі числення.
Крайні ліві нулі в цілій частині та крайні праві нулі у дробовій частині можна на папері не писати, тобто те ж саме десяткове число у двійково-десятковій системі числення можна записати так: 11000011000,011101.
Чотири двійкових розряди називають тетрадою.
Щоб знайти десятковий еквівалент двійково-десяткового числа, потрібно в цілій частині ліворуч від коми й у дробовій частині праворуч від коми виокремити тетради і знайти їх десяткові значення. Неповні тстради доповнюються нулями.
Приклад:
0100 1000 1001, 0101 0010-двійково-десяткове подання
489,52
Подане двійково-десяткове число дорівнює десятковому числу 489,52.
Щоб розрізняти, в якій системі подано число, праворуч від нього в дужках (або просто в нижньому індексі) інколи записують систему числення. Наприклад: 101001(2); 1011001,011001<2-ю)- Перше число, записане в двійковій системі числення, а друге — у двійково-десятковій системі.
Таблиця 1.3
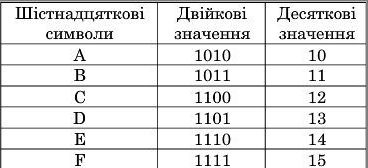
Перших десять символів (цифр) шістиадцяткової системи числення збігаються з цифрами десяткової системи, а інші символи позначаються латинськими літерами А, В, С, Б, Е, Е. У табл. 1.3 подано ці символи й відповідні їм двійкові та десяткові значення. Наведено кодування десяткових і шістнадцяткових символів двійковими значеннями, у яких розряди мають значення (вагу) 8, 4, 2, 1. Такий код (8421) називають кодом прямого заміщення. На практиці ніколи використовзлоться інші коди, застос\шання яких визначається специфікою задач.
Перевіряємо себе
1. Чому двійкова система е основною в обчислювальній техніці?
2. Як нумеруються розряди числа?
Поясніть, як отримується значення числа в нспозиційних
системах числення.
4. Як відображаються значення десяткових цифр у двійковій системі числення?
Чи потрібна цифра 8 для відображення чисел у вісімковій системі числення?
6. Як записуються значення шістнадцяткових цифр у двійковій системі?
7. Як запшуються десяткові числа у двійково-десятковій системі?
У якій системі числення подано число 1024.75 ? Чому не можна дати однозначну відповідь на це запитання?
9. Навіщо й чому в шістиадцятковій системі числення використовують ЯК цифри літери х\— Р?
Виконуємо
1. Запишіть десяткове число 93,64 у вигляді суми значень його розрядів.
2. Запишіть двійкове число 110111,011 у вигляді суми значень його розрядів (у десятковій системі числення).
3. Запишіть десяткове число 170,25 у двійково-десятковій системі
числення.
4. Доведіть, чому запис 1011110111,011110 не може бути двійково-десятковим поданням числа.
Результат обчислень 1-24 + 0-23 + 1-22 + 0-21 + 1-2° + 0-21 + 1-22 запишіть двійковій системі числення.
V,. —Двійково-десяткове число 1011000,00100101 запишіть у десятковій системі числеїшя, а після цього — у вигляді суми значень його
розрядів.
Шістнадцяткове число А0Е,В запишіть у двійковій системі
числення.
Чому запис числа 1011101101,00100101 не може бути двійково-десятковим поданням?
1.3. Арифметичні дії в позиційних системах числення
Арифметичні операції в позиційних системах числення, в тому числі у двійковій системі, виконуються за тими ж правилами, за якими вони ВИКОІІЗТОТЬСЯ в десятковій системі числення.
Очевидно, що при цьому використовуються таблиці додавання й таблиці множення для тієї системи числення, в якій виконуються певні операції. Додавання чисел здійснюється послідовно, розряд за розрядом, починаючи з молодшого розряду, з перенесенням з розряду в розряд одиниць старшого розряду числа, що є сумою значень розрядів, які додаються.
Приклад. Додати двійкові числа 10111,01 і 110,111.

Приклад. Помножити двійкові числа 101,01 на
11,01.

У наведеному прикладі множення почалося з молодшого розряду множника, а часткові добутки зсувалися ліворуч. У комп’ютерах множення інколи виконується починаючи зі старшого розряду7 множника, при цьому часткові добутки зсуваються праворуч. Наприклад, ті ж самі числа можна помножити і так:

Приклад. Розділити двійкове число 1000010 на двійкове число 110.
Перевіряємо себе
1. За якими правилами виконуються арифметичні операції 5' двійковій системі числення?
2. Наведіть приклад додавання двох чисел у двійковій системі числення.
3. Наведіть приклад множення двох чисел у двійковій системі числення.
4. Наведіть приклад ділення двох чисел у двійковій системі числення.
Виконуємо
1. Додайте двійкові числа 100111,011 і 1111,001.
2. Від двійкового числа 100001,01 відніміть двійкове число 1101,011.
3. Помножте двійкове число 1101,01 на двійкове число 101,11.
4. Поділіть двійкове число 1110101 на двійкове число 1101.
Додайте вісімкові числа 57,3 і 26,1 і відніміть від першого друге.
Поділіть шістнадцаткове число А0(ів) на число 14<ц>), відніміть від числа АО (їв) число 14(ю).
Додайте й помножте двійкові числа 110,1 і 1011,01.
Поділіть двійкове число 10000010 на двійкове число 1010 і від першого відніміть друге.
1.4. Перетворення подання чисел із однієї системи числення в іншу
У комп’ютерах перетворення подання чисел із однієї системи числення в іншу здійснюється автоматично за допомогою спеціальних програм або електронних схем. Існують різні методи перетворення подання чисел.
Перший метод можна вважати універсальним, тобто придатним для цілих, дробових і мішаних чисел.
Нехай число А, у якому в цілій частині міститься /г-розрядів, а в пгтбовій — т-розрядів, подано в системі числення з основою д.
Алгоритм перетворення подання числа в системі числення з основою д (А/д)) на подання цього числа в системі числення з основою р <А(р)).
1. Число А(д) записати у вигляді суми значень його розрядів:
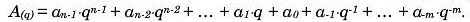
2. Основу системи д і всі числа <ц, записати в системі числення з основою р.
3. Виконати арифметичні операції кроку 2 в системі числення з основою р.
Приклад. Двійкове число 11011,01 подати в десятковій системі числення.
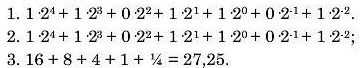
Приклад. Десяткове число 21,5 подати у двійковій системі числення.
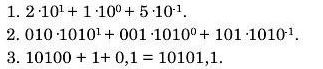
Другий метод перетворення подання чисел із однієї системи числення в іншу називається методом ділення на основу. Він придатний ТІЛЬКИ ДЛЯ ЦІЛИХ чисел. Нехай ЦІЛО ЧИСЛО А(я) потрібно перевести в систему з основою р. Перетворення здійснюється за таким правилом.
Число А(ч) ділиться на нову основу (р), яка представлена в системі q. Отримаємо остачу і цілу частину. Якщо ціла частина не менша за р, вона також ділиться на р. Цей процес здійснюється доти, доки остання остача стане менше р. Остачі від ділення — це і є цифри числа А за основою р. При цьому молодшою цифрою є перша остача, а старшою — остання.
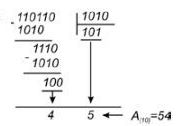
Приклад. Число Дч >= 110110 подати в десятковій системі числення.
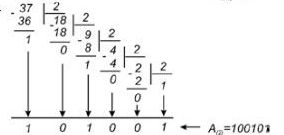
Приклад. Число Дц>) = 37 подати у двійковій системі числення.
Третій метод називається методом множення на основу. Вій використовується лише для дробових чисел. Перетворення здійснюється за таким правилом.
Помножити число А на основу р, яка подана в системі числення з основою q. Отримаємо цілу частин}' й дріб. Дріб також множиться на основу р. Знову отримаємо цілу частину й дріб. Процес множення продовжується доти, доки дріб стане рівним нулю або меншим від числа, заданого як точність подання. Множення виконується в системі числення з основою q. Цифри, що відповідають цілим частинам чисел, які отримуються в процесі множення, і є цифрами числа А в системі з основою р.
Приклад. Число А(щ = 0,375 подати у двійковій системі числення.

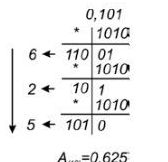
Приклад. Число А(ч) = 0,101 подати в десятковій системі числения.
Якщо основа першої системи числення є цілим степенем основи другої системи числення, то перетворення подання чисел між системами суттєво спрощується. Зокрема, такими системами є двійкова та шістпадцяткова системи числення (24 = 16).
Приклад. Число А^щ = 4Е5,СА у двійковій системі мас такий запис:
А2)= 10011100101,1100101.
Щоб записати двійкове число в шістнадцятковій системі числення, треба в його лівій частині ліворуч від коми й у дробовій частині праворуч від коми виокремити по 4 двійкових розряди і знайти їх подання в шістнадцятковій системі.
Приклад. Число А^і) = 101010000101,11011 у шістнадцятковій системі має запис Ац6) = х\85,Б8.
Перевіряємо себе
1. Сформз'люйте правило перетворення подання чисел із однієї системи числення в іншу методом ділення на основу.
2. Сформулюйте правило перетворення подання чисел із однієї системи числення в іншу методом множення на основу.
3. Сформулюйте правило перетворення подання чисел із однієї системи числення в іншу універсальним методом.
4. У чому полягає особливість перетворення подання чисел із однієї системи числення в іншу' для систем, у яких основа однієї є цілим степенем основи іншої системи числення?
Виконуємо
1. Подання числа А(ч) = 101011,1 переведіть в десяткову систему числення.
2. Подання числа Ацо) = 75,375 переведіть у двійкову систему числення.
3. Подання числа А(к>) = В 1,7 переведіть у двійкову систему числення, а з
двійкової - у десяткову.
4. Подання числа = 57,625 переведіть у десяткову систему числення, а з десяткової — у двійкову.
Подання числа А<2-іо) = 10010001,011000100101 переведіть у двійкову систему числення, а з двійкової — у нгістнадцятковз'.
Подання числа А<н>) = 140,75 переведіть у игістиадцяткову систему числення, з неї — у двійкову, а з двійкової — в десяткову.
Знайдіть десяткове значення суми чисел А/2) = 111001.001 і
В(2) — 11101,01.
Знайдіть двійкове значення с^тии чисел Ар») = 28,375 і
В(8)= 44,3.
1.5. Способи подання чисел у обчислювальній техніці
Основні вимоги до технічної реалізації арифметичних операцій над числами - це простота електронних схем, мінімальні апаратні витрати, висока швидкість і надійність виконання операцій.
Оскільки операції віднімання, множення й ділення фактично зводяться до виконання операції додавання, то технічно реалізувати таку задачу досить просто.
Зокрема, вона реалізована в пристрої, який отримав назву АЛБ -арифметично-логічний блок. Використання такого блока для виконання обчислень призвело до необхідності розроблення спеціальних методів подання двійкових чисел.
Поширені три основних способи (коди) подання двійкових чисел. Далі користуватимемося такими назвами: прямий код (або значення зі знаком); зворотний код (або доповнення до одиниці); додатковий код (або додаваішя до двох).
Для всіх перелічених способів крайній лівий розряд (старший розряд) у цілій частині числа дорівнює нулю для додатних чисел і одиниці - для від'ємних чисел. Надалі під час запису на папері знаковий розряд від інформативних відокремлюватимемо крапкою, а коди позначатимемо так: прямий — індексом пк, зворотний — індексом зк, додатковий — індексом дк, наприклад, Апк, А™, Адк. Додатні числа в усіх трьох кодах мають однакове зображення, від'ємні — різне.
Прямий код зазвичай використовується в процесі введення
та виведення числових даних із комп'ютера, а також під час .зберігання чисел у пам'яті комп'ютера.
У прямому коді числа подаються так само, як і в звичайній формі, лише замість знака "+" у знаковому розряді записується нуль, а замість знака у цей розряд записз'ється одиниця. Наприклад, двійкове число 10110,01 у прямому коді записується так: Апк= 0.10110,01, а від'ємне число -100011,101 - у такому вигляді: АпК = 1.100011,101. Число нуль у прямому коді має два зображення: 0.00...0,0...0 і 1.00...0,0...0.
Зауважмо, що знаковий розряд у прямому коді несе інформацію тільки про знак числа і не мас ніякого кількісного значення, тобто його вага дорівнює нулю.
Зворотний і додатковий коди позбавлені цього недоліку, тобто додавання та віднімання реалізується однією електронною схемою. Для цього перед викопаїшям операції віднімання знак числа, що віднімається, змінюється на протилежний. Наприклад, (А) — (В) = = (А) + (-В); (А) - {-В )= (А) + (В ).
Зворотний код. Знаковий розряд від'ємного числа ліас
від'еліиу вагу — (2п-2-т), де п - кількість розрядів у цілій частині, т -кількість розрядів у дробовій частині.
Таке значення ваги обрано не випадково. З одного боку, воно забезпечує дуже простий перехід від прямого коду до зворотного й навпаки, а з іншого - дає змогу виконувати операцію додавання над кодами чисел за звичайними правилами. При цьому знакові розряди бепуть участь у додаванні так само, як і іпсЬооманійпі оозпяди.
Для перетворення подання від'ємного числа із прямого коду в
зворотний необхідно знаковий розряд залишити оез зміни, а в кожному інформаційному розряді замінити одиниці на нулі, а нулі - на одиниці.
Приклад. Число, зображене в прямому коді як Апк= 1.10010,011 , у зворотному коді зображається так: Азк=1.01101,100. Для перетворення зворотного коду' від’ємного числа на прямий код виконуються аналогічні дії. Наприклад, число в зворотному коді А™ = 1.01001,010 у прямому має значення А*к =1.10110.101.
Додавання чисел у зворотному коді виконується за звичайним
правилом додавання, а саме: додавання починається з молодших розрядів із врахуванням одиниць перенесення з розряду в розряд. Одиниця перенесення, яка виїшкає зі знакового розряду, переноситься в наймолодший розряд раніше отриманої суми і додається до неї.
Кількість розрядів чисел, які додаються, мас бути однаковою в обох числах. Вирівнювання кількості розрядів необхідно виконувати в прямому коді.

Приклад. Додати в зворотному коді числа А( ч) В(2) = 110001,11. Урівнюємо кількість розрядів чисел у прямому коді: Апк = 1.010111,01 і Впк = 0.110001,11. Перетворюємо числа у зворотний код і виконуємо їх додавання:
Додатковий код. Вага знакового розряд}' від’ємних чисел додаткового коду від'ємна і дорівшоє -2п.
Для перетворення прямого коду від'ємного числа на
додатковий код необхідно отримати його зворотний код, до молодшого розряду якого додати одиницю.
Приклад. А(ч) = -10010,01 записати в додатковому коді: АпР = = 1.10010,01 -»А.™ = 1.01101,10-» А* = 1.01101,11.
Для отримання прямого коду з додаткового необхідно отримати його зворотний код (для цього слід відняти одиницю з молодшого розряду' додаткового коду) й зі зворотного коду отримати прямий код. Приклад: Адк= 1.001010,011 -» А**= 1.001010,010 -» А™ = 1.110101,101.
Недоліком розглянутого методу' є те, що для отримання прямого коду потрібно виконувати операцію віднімання. На практиці використовується інший метод, який полягає у створенні додаткового коду' від додаткового. Тобто спочатку створюється зворотний код від додаткового, а потім до його молодшого розряду' додається одиниця.
Зазначимо, що в комп'ютерах кількість розрядів у схемах для додавання фіксована. Тому під час додавання двох чисел однакових знаків результат може бути більшим від максимального числа, яке можна записати в розрядну сітку. У цьому випадку результат буде неправильним. Таке явище називається переповненням розрядної сітки.
Приклад. Додати числа Д2) = 110,01 і В(ч) = = 11,111.

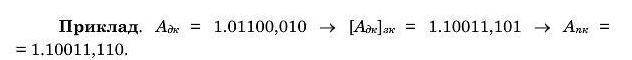
Додавання чисел у додатковому коді виконується так само, як і в зворотному коді, однак одиниця перенесення, що виїшкас зі знакового розряду, відкидається.

У наведеному прикладі додавалися два додатних числа, а результат - від ємний. Це означає, що настало переповнення розрядної сітки. Для виявлення переповнення розрядної сітки використовз'ється спеціальна схема — індикатор, що аналізує знаки чисел і знак суми. Якщо обидва числа мають однаковий знак, а знак суми інший, то ця схема видає сигнал переповнення розрядної сітки й обчислення припиняється.
У додатковому коді простіше виконується операція додавання, тому що не потрібно здійсшовати циклічне перенесення одиниці в молодший розряд. Саме цей чинник і сприяв тому, що в сучасних комп'ютерах використовується додатковий код.
Перевіряємо себе
1. Сформулюйте правило запису чисел у прямому коді.
2. Наведіть правило перетворення чисел із прямого коду на зворотний і навпаки.
3. Сформулюйте правило додавання чисел у зворотному коді.
4. Наведіть правило перетворення чисел з прямого коду на додатковий і навпаки.
5. Сформулюйте правило додавання чисел у додатковому коді.
Виконуємо
1 .Числа А(2)= 101,1 і В(2) = —1001,01 запишіть у зворотному й додатковому кодах.
У математиці використовуються природна (з фіксованою комою) і нормальна (з плаваючою комою) форми подання чисел. У природній формі число подасться у вигляді цілої і дробової частин, між якими ставиться кома. Ці ж самі форми подання чисел використовуються і в обчислювальній техніці.
У нормальній формі число зображається у вигляді мантиси й порядку. Наприклад, число А = 101011 може бути записане так: 0,00101011.2Ш)0, 0,101011.2і10 або 1,01011.2і01 та ін. Останній запис означає, що число нормалізоване.
Нормалізованими називаються числа, в яких кома стоїть праворуч після першої значущої цифри, тобто у двійковому записі завжди після одиниці. Головна перевага нормалізованої форми полягає в тому, що ліворуч від коми завжди стоїть одиниця.
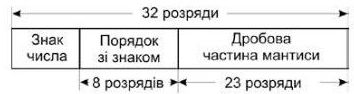

Для допитливих
Рис. 1.1. 32-розрядне подання числа з плаваючою комою Перевага подання чисел із фіксованою комою, порівняно з плаваючою комою, полягає в тому, що в ньому значно простіше виконуються арифметичні операції. Нормалізована форма дає
змогу за однієї й тієї ж кількості розрядів представити значно більший діапазон чисел.
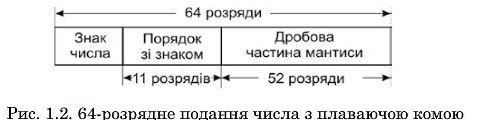
У сучасних комп’ютерах числа з фіксованою і плаваючою комами найчастіше подаються в форматі стандарту IEEE (англ.: Institute of Electrical and Electronics Engineers). Цей стандарт визначає не лише форми подання чисел, а й правила виконання арифметичішх операцій, правила перетворення подання чисел із десяткового у двійкове і навпаки та інші дії над числами. Стандарт IEEE визначає дві форми подання чисел із плаваючою комою: з 32 розрядами (рис. 1.1) — її називають формою з одинарною точністю, і з 64 розрядами (рис. 1.2) - її називають формою з подвійною точністю.
У полі порядку 32-розрядного формату замість числа зі знаком зберігається ціле число без знака з надлишком 127. Наприклад, якщо реальний порядок дорівнює 5 (у двійковій системі 101), то він буде записаний у вигляді 10000100. Оскільки мантиса подається в нормалізованому вигляді, то найстарший біт явно не вказується, розуміється, що в ньому завжди одиниця.
З урахуванням описаного в розрядній сітці, зображеній на рис. 1.3, записано число 1,011010...0.10^8.

Порядок у форматі 64 розрядів мас надлишок 1023. 11-розрядиий порядок відповідає десятковому порядку приблизно 10+:,,)8, а 53-розрядиа мантиса забезпечує майже таку ж точність, як і 16 десяткових цифр.
|
Практична робота № 1 |
Тема: |
Перетворення чисел із десяткової системи числення в іншу і навпаки, з двійкової в шістнадцяткову і навпаки. Операції над числами в двійковій і шістнадцятковій системах числення |
|
Мета: |
Набути практичних навичок подання й порівняння чисел у системах з різними основами |
1. Число .А(іо) = 107,625 перетворити у двійкову, шістнадцяткову та двійково-десяткову системи числення.
4. Над числами Д») = 1011011,101 і В&) = 11101,01 виконати операції додавання і множення. Від числа А відняти число В.
2. Число Д2> = 101011101,0011 перетворити в десяткову, шістнадцяткову та двійково-десяткову системи числення.
3. У режимі on-line перевірити правильність виконання операцій над числами, наведеними у п. 2 і п. 3. Скористайтеся для цього одним із сайтів, наприклад, http:// math-ua.semestr.ru/iniyindex.php (рис. 1.4).

5. Розділити число А(2) = 100011000 на число В(2) = 1110.
6. У режимі on-line перевірити правильність виконання операцій над числами, наведеними в п. 4 і п. 5. Використайте для цього, наприклад, сайт https://www.numsys.пі/.
7. Виконати операцію додавання в додатковому та зворотному кодах над числами А(2> = 10001010,001 і В<2) = -1011,01.
Словничок
|
Система числения |
- сукупність правил запису (зображення) чисел за допомогою символів (цифрових знаків) і виконання операцій над ними |
|
Розряд числа |
- номер позиції цифри в записі числа |
|
Основа системи числення |
- кількість цифр, які можуть використовуватися у кожному розряді числа |
|
Вага розряду |
- основа системи числення в степені номера розряду |
|
Двійкова система числення |
- позиційна система числення зі символами 0 і 1 |
|
Кількісне значення цифри |
- значення цифри, помножене на вагу розряду' |
|
Тетрада |
- чотири двійкових розряди |
|
Прямий код числа |
- запис числа в звичайній формі зі знаковим розрядом |
|
Зворотний код числа |
- код, за допомогою якого можна замінити операцію віднімання на операцію додавання |
|
Додатковий код числа |
- код, додатні числа якого збігаються зі зворотним кодом числа, а від’ємні відрізняються на одиницю молодшого розряду |
Це матеріал з підручника Інформатика 8 клас (поглиблений рівень) Гуржій
Автор: admin от 12-12-2016, 21:56, Переглядів: 11007