Квадратні корені і дійсні числа,
Квадратний корінь і його перетворення
Поняття квадратних коренів числа виникло близько 4 тисяч років тому у Вавилоні. Перехід від визначення площі квадрата за його стороною до оберненої дії — пошуку сторони квадрата за його площею, призвів до розвитку розділу математики про квадратні корені. Ще у Вавилоні були складені таблиці квадратів чисел і величини квадратних коренів із числа. Щоправда, обчислення були наближеними. Детальний метод добування квадратних коренів був описаний лише у І столітті дон. е. давньогрецьким ученим Героном Олександрійським.
Означення. Квадратний корінь із числа а — де число b\ яке, будучи піднесеним до квадрата, дорівнює числу а. Квадратного кореня із від’ємного числа не існує. Квадратний корінь із числа 0 дорівнює 0.
Квадратний корінь із додатного числа має два значення: додатне і протилежне йому від’ємне число.
Невід’ємне значення квадратного кореня називають арифметичним квадратним коренем із числа.
Обчислення арифметичного значення квадратного кореня називається добуванням квадратного кореня.
Означення. Арифметичним квадратним коренем із числа а називається таке невід’ємне число, квадрат якого дорівнює а.
Знак арифметичного кореня -
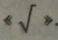
Арифметичний квадратний
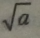
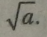 |
Вираз |
має смисл лише при а >= 0.
правильна лише тоді, коли виконуються такі умови: 1 )Ь>
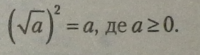
І Із означення арифметичного квадратного кореня виходить, що рівність
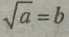
0; 2) Ьг і а.
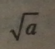
Отже, якщо а > 0, то існує два квадратних корені з цього числа: (арифметичний квадратний корінь) і —
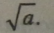
|
Квалпатним копенАм із числа 49 єчисла х = 7 і = —7. оскільки |
 |
|
Точно добути квадратний корінь можна лише з числа або виразу, які подано степенем, показник якого кратний 2, з раціональною основою. Коре- |
ні квадратні інших чисел добуваються наближено (із визначеною умовною точністю).
Так, л/3 означає таке додатне число х, квадрат якого дорівнює 3.
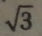
І2 - 1,22 - 4, а 1 < 3 < 4, тоді арифметичний квадратний корінь із трьох — це число, яке знаходиться між натуральними числами 1 і 2, тобто число дробове. Спробуємо дібрати число, квадрат якого дорівнює 3. Нескінченний періодичний дріб 1,7320508... відповідає цій умові.
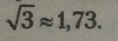
Прийнято вважати V3 «1,73.
Таблиця квадратів натуральних чисел від 10 до 99 дозволяє знаходити як квадрати чисел від 1 до 99, так і чисел, що являють собою десяткові дроби, у яких один розряд до коми і один розряд після коми. Відповідно, за ЦІЄЮ таблицею можна добувати квадратні корені натуральних чисел від 1 до 99 або раціональних чисел з одним знаком після коми. У випадку раціональних чисел у полі таблиці беремо число, уявно ставимо кому, відділивши два розряди справа, шукаємо число десятків і одиниць, і в одержаному числі відділяємо комою від цілої частини один розряд справа.
Приклади.

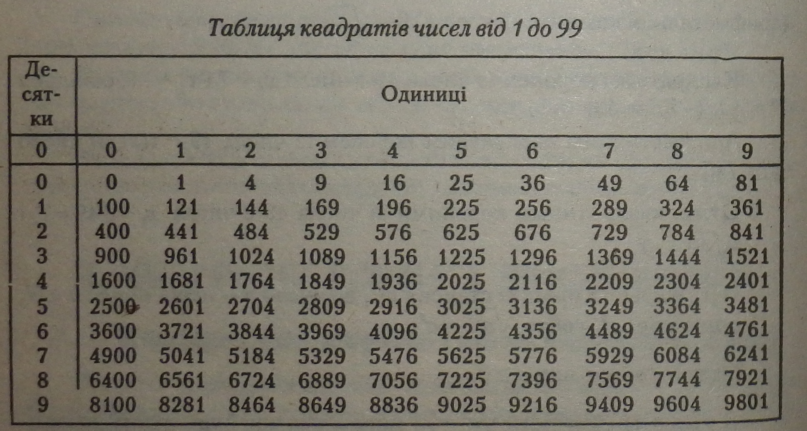
у в а г а! Не можна добувати корінь із кожного доданка (зменшуваного і від’ємника) окремо.
Приклади.
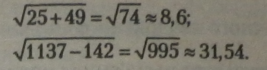
Щоб добути квадратний корінь із добутку (частки), можна добути квадратний корінь із кожного множника (діленого і дільника), а одержані значення узяти добутком (часткою).
Приклади.
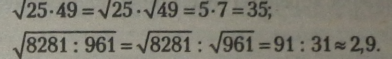
Щоб добути квадратний корінь із дробу, потрібно добути квадратний корінь із чисельника і знаменника окремо, а одержані значення залишити дробом або обчислити як частку (якщо це можливо за умовою). Приклад.
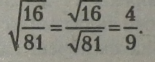
З-під знаку кореня можна винести множник і можна внести множник під знак кореня. При винесенні множника із нього добувається корінь, а при внесенні він підноситься до відповідного степеня. Приклади.
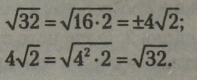
Якщо корінь у знаменнику дробу, то такий дріб можна замінити тотожним йому дробом, який не містить радикалів (коренів) у знаменнику. Для цього множать чисельник і знаменник дробу на такий вираз (спряжений знаменнику), у якому корінь у знаменнику добувається.
Приклади.
1. Позбутися радикала у знаменнику дробу:
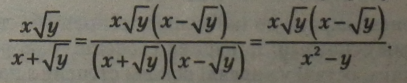 |
|
2. Позбутися радикала у знаменнику дробу: |
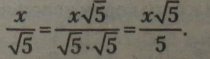
|
3. Позбутися радикала в чисельнику дробу: |
 |
Означення. Звільнення дробу від радикалів у чисельнику (знаменнику) дробу називається перетворенням дробу.
Властивості арифметичного квадратного кореня
1. Квадратний корінь із добутку двох невід’ємних множників дорівнює добутку коренів із цих множників.
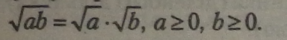
3. Квадратний корінь із дробу, чисельник якого невід’ємний, а знаменник додатний, дорівнює кореню із чисельника, поділеному на корінь із знаменника.
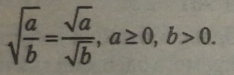
Щоб перетворити суму (різницю) квадратних коренів, треба звести підкореневі вирази до однієї основи степеня, якщо це можливо, добути корені із степенів і записати їх перед знаками коренів, а ті квадратні корені, що залишилися, з однаковими підкореневими виразами можна додати, для цього складаються коефіцієнти перед знаком кореня і дописується той самий корінь.
Приклади.
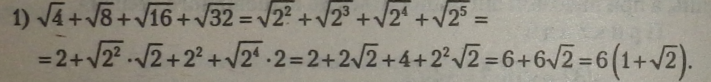 |
|
Зведемо всі підкореневі вирази до основи 2. Із парного степеня корінь добувається повністю, із непарного степеня корінь основи в степені 1 залишаємо під знаком кореня. Зводимо подібні цілі.числа і коефіцієнти складаємо з однаковими коренями. Запишемо двочлен як добуток числа і двочлена суми. |
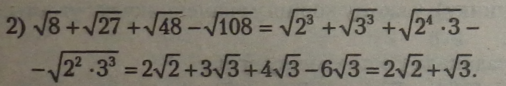
Зводимо підкореневі вирази до найменшої основи або добутку степенів з найменшими основами. Із парних степенів підкореневих виразів добуваємо корінь, остачі у вигляді основи степеня з показником 1 або добутком таких основ залишаємо під знаком кореня. Зводимо подібні члени (складаємо коефіцієнти в однакових коренів).
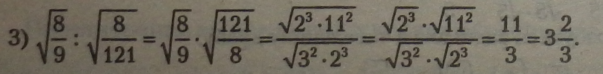 |
|
Замінимо ділення дробів на множення (із заміною другого дробу на обернений). Перемножимо окремо чисельники і знаменники дробів. Під |
кожним знаком кореня виділимо степені. Скоротимо однакові множники у чисельнику і знаменнику. Добудемо корені із парних степенів.
Розглянемо перетворення квадратних коренів і виразів з квадратними коренями на прикладах.
Приклади.
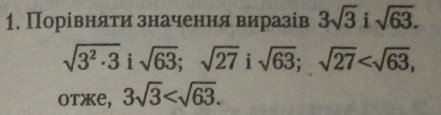
Щоб порівняти два квадратних корені, їх підкореневий вираз потрібно звести до степеня з однаковою основою, тоді чим більший показник степеня підкореневого виразу, тим більше значення квадратного кореня.
У цьому прикладі звести до одної основи підкореневі вирази не можна, бо в першому корені основа 3, а в другому — 3 і 7.
Другий спосіб порівняння полягає в тому, щоб внести коефіцієнт кореня у підкореневий вираз і порівняти числові значення підкореневих виразів. Чим більший підкореневий вираз у квадратного кореня, тим більше його числове значення.
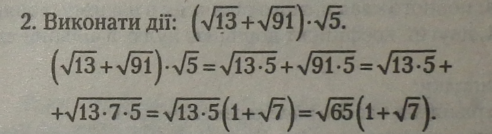
Використовуючи розподільний закон множення і правило множення коренів з однаковими показниками (у нашому випадку — квадратних коренів), дістали суму двох квадратних коренів із добутком під знаком кореня. Розкладемо 91 на прості множники і винесемо корінь за дужки із спільними підкореневими множниками (13 • 5).
Ми дістали добуток кореня і двочлена, у якого один із одночленів ціле число (1).
 |
|
У підкореневих виразах виділимо множниками числа, з яких можна добути цілий квадратний корінь. Добудемо квадратні корені із степенів і поставимо числа коефіцієнтами квадратних коренів. У членів даного многочлена є спільний множник >/§, який можна винести за дужки. Зведемо подібні доданки. |
за формулою
скороченого множення можна записати як різницю квадратів основ.
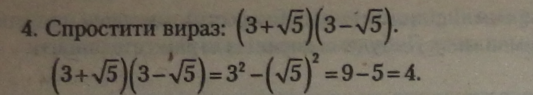 |
|
Добуток суми і різниці двох однакових основ |
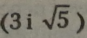
Корінь квадратний у квадраті завжди дорівнює підкореневому вира* зу, тому ми позбудемося радикала (знаку кореня) у виразі.
— це неповне рівняння другого степеня, або неповне квадратне рівняння.
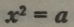
Означення. Рівняння
Повне квадратне рівняння має вигляд:
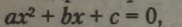
де а, b і с — деякі числа або коефіцієнти квадратного рівняння, причому а*0;а — перший коефіцієнт, Ь — другий коефіцієнт, а с — вільний член.
Неповне квадратне рівняння вигляду х* = а замінимо на рівносильне х? - а - 0. За видом повного квадратного рівняння в нашому рівнянні перший коефіцієнт 1, другий коефіцієнт дорівнює нулю, а вільний член дорівнює -а.
Можливі три випадки:
1. Якщо а *= 0, то рівняння має два рівні корені. хх - х2 - 0.
2. Якщо а > 0, то рівняння має два корені, один із них додатний, другий — від’ємний, а модулі коренів — рівні:
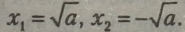
3. Якщо а < 0, то рівняння не має коренів.
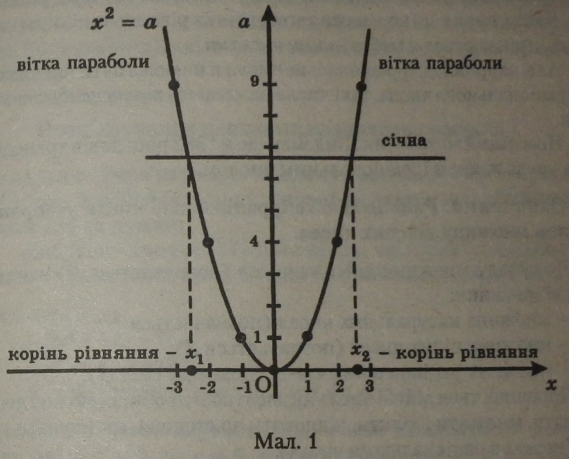
Графіком рівняння а = я2 є парабола.
Якщо х - 0, то і а в 0, тому парабола має вершину в точці початку координат О (0; 0). Вітки параболи спрямовані вгору, оскільки коефіцієнт при Xі дорівнює 1 (додатний).
Парабола будується табличним способом (заданим довільно числовим значенням х повинні відповідати числові значення а, які обчислюються за рівнянням параболи).

За точками, взятими з таблиці, побудуємо параболу в плоскій системі координат. Оскільки система координат на площині показує залежність двох змінних (х і у), одна з яких незалежна (.х), а друга — залежна {у) від першої змінної (*).
|
у заданому рівнянні роль залежної змінної (у) виконує а. Дві точки параболи, що перетинається із січною, яка лежить у тій зсе системі координат паралельно осі х, будуть мати координати на осі абсцис xt і ху модулі яких дорівнюють |
 |
|
Така парабола називається ще квадратичною параболою (або графіком квадратичної функції). |
2.3. Поняття ірраціонального числа
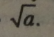
Цілі числа і дроби (додатні і від’ємні) складають раціональні числа. Цих чисел достатньо для практичних вимірів будь-яких величин, але недостатньо для теорії вимірів.
Інші числа, що є довжинами відрізків, несумірні з будь-яким одиничним відрізком довжини і називаються ірраціональними. «Ірраціональ-' ний» дослівно перекладається «той, що не має відношень». Так, відношення діагоналі квадрата до його сторони представлене числом >/2, яке і є ірраціональним числом (його не можна точно вирахувати, тому що це нескінченний неперіодичний дріб).
Означення. Числа, які не можна представити у вигляді неско
|
ротного дробу |
 |
називаються ірраціональними. Будь-яке ірраціональне число можна представити у вигляді нескінченного десяткового неперіодичного дробу.
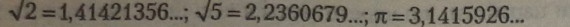
Якщо обчислення кореня квадратного приводить до нескінченного неперіодичного дробу, то квадратний корінь такого числа (його ще називають радикалом) є ірраціональне число, яке виражене через радикал.
Числа, виражені коренями алгебраїчних рівнянь із цілими коефіцієнтами, називаються алгебраїчними числами.
Але, наприклад, ірраціональне число п не може бути виражене коре-нем-раціонального числа, такі числа називають трансцендентнимичислами.
Німецький математик Ліндеман ще в 1882 році довів трансцендентність числа п, яке є ірраціональним числом.
Означення. Раціональні та ірраціональні числа утворюють разом множину дійсних чисел.
До складу множини дійсних чисел (позначається R) входять такі числові множини:
— множина натуральних чисел (позначається N);
— множина цілих чисел (позначається Z);
— множина раціональних чисел (позначається Q).
Порівнюються дійсні числа як десяткові дроби. їх можна додавати і
віднімати, множити і ділити, підносити до степеня, записувати як радикали (корені з раціонального числа).
Автор: admin от 8-06-2013, 22:39, Переглядів: 113674