Системи лінійних рівнянь з двома змінними, Лінійні рівняння з двома змінними, способи розв'язування рівнянь з 2 змінними
Лінійні рівняння з двома змінними
Означення. Лінійні рівняння з двома змінними — це рівняння типу ах + by = с, де х і у — змінні, а а, Ь, с — певні числа, постійні для заданого рівняння.
Лінійними такі рівняння називаються тому, що змінні в них мають показник у першому степені.
Приклад.
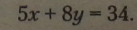
Правило. Розв’язком рівняння з двома змінними називається пара значень змінних, яка перетворює рівняння в правильну числову рівність. Ця пара значень змінних називається розв'язком рівняння.
Якщо задано одне рівняння з двома змінними, то у нього буде безліч розв'язків, оскільки не одна пара чисел перетворює дане рівняння в тотожність (правильну рівність).
Приклади.
З*-2у“11.
При дг *= 5 і у - 2 рівняння перетворюється в правильну рівність: 3*5 — 2*2 = 11; 11 = 11- тотожність.
При х = 6 іу = 3,5 рівняння перетворюється в правильну рівність: З • 6 - 2 • 3,5 = 11; 11 = 11 — тотожність.

Властивості лінійного рівняння з двома змінними
1. Якщо в рівнянні виконати тотожні перетворення якоїсь його частини (звести подібні доданки, розкрити дужки), то одержимо рівняння, рівносильне даному.
2. Якщо в рівнянні перенести доданок з одної частини у другу, змінивши знак на протилежний, то одержимо рівняння, рівносильне даному.
3. Якщо обидві частини рівняння розділити або помножити на одне й те саме число, відмінне від нуля, то одержимо рівняння, рівнозначне даному.
Приклади.
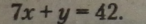
|
Нехай х - 5 і у - 7 — корені рівняння, тоді |
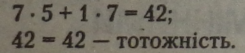 |
|
Деренесемо другий доданок зліва направо: |

|
при х - 5 і у “ 7 рівняння перетворюється на вірну рівність: |
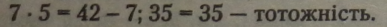 |
|
Перенесемо перший доданок зліва направо: |
 |
|
Помножимо обидві частини рівняння на (-1): |


Розв'язування лінійних рівнянь з двома змінними
Оскільки лінійне рівняння з двома змінними має безліч розв’язків, то одному з невідомих (х або у) надається певне значення, яке підставляється в рівняння замість букви, тоді друге невідоме можна обчислити, розв’язавши рівняння як рівняння з одним невідомим.
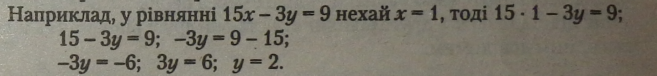
Наприклад, у рівнянні 15* - Зу * 9 нехай х * 1, тоді 15 • 1 - Зу * 9; 15-3у = 9; -3у * 9 - 15;
-Зу = -6; Зу - 6; у = 2.
Підставимо в рівняння у = 2 і зробимо перевірку:
15-1-3-2 = 9;9“=9 — тотожність.
Рівняння розв’язане правильно.
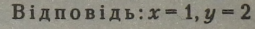
Відповідь:*** 1,і/ = 2 (або можна записати так: (1; 2».
Правило. Оскільки лінійне рівняння з двома невідомими має безліч розв’язків, то, щоб розв'язати рівняння, треба надати числове значення одному з невідомих, підставити його в задане рівняння й обчислити значення другого невідомого, як у лінійному рівнянні з одним невідомим.
Пара лінійних рівнянь з двома невідомими, які мають спільний розв’язок, називається системою лінійних рівнянь.
Розв'язування системи лінійних рівнянь з двома змінними
Означення. Якщо два невідомих зв’язані не одним, а двома рівняннями, то ці рівняння складають систему лінійних рівнянь з двома змінними.
Розв'язком системи рівнянь з двома змінними називається пара чисел, при яких кожне рівняння системи перетворюється на правильну числову рівність.
Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що система розв’язків не має.
Записуючи систему двох рівнянь, ці два рівняння об’єднують фііурною дужкою.
|
Приклад. |
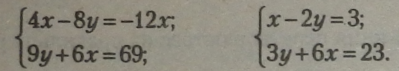 |
Дві системи рівнянь називаються рівносильними, якщо кожна з них має ті самі розв’язки, що й інша.
Системи лінійних рівнянь з двома змінними розв’язуються одним із трьох способів:
1. Графічно — в одній системі координат будуються графіки двох рівнянь, і координати точки перетину графіків відповідають кореням рівнянь.
2. Способом підстановки — в одному рівнянні виражають перше невідоме через друге (або навпаки — друге через перше), а потім його значення підставляють у друге рівняння, дістаючи друге рівняння як рівняння з одним невідомим.
3. Способом алгебраїчного додавання — в обох рівняннях, використовуючи основні властивості рівнянь, урівнюються коефіцієнти при одному з невідомих так, що вони мають протилежні знаки (знаки «+> і«-») і однакові чисельно. Рівняння почленно додаються і сума коефіцієнтів при одному з невідомих перетворюється на нуль, тим самим перетворюючи на 0 весь одночлен.
Записавши нове рівняння (суму системи рівнянь), ми одержуємо лінійне рівняння з одним невідомим, розв’язуючи яке, знаходимо його корінь. Це числове значення невідомого підставляємо в будь-яке з двох рівнянь і обчислюємо числове значення другого невідомого.
Усі три способи розв’язування рівнянь рівноцінні але кожний має свої особливості:
1. Графічний спосіб — найбільш наочний, але має й найбільші похибки при обчисленнях, оскільки точність визначення координат точки залежить від масштабу зображення. Особливо складним є розв’язування систем, коли коефіцієнти або корені рівнянь — дробові числа.
2. Спосіб підстановки — найбільш універсальний з усіх способів розв’язування лінійних рівнянь з двома невідомими. Він використовується
практично для всіх типів систем рівнянь (цілих і дробових), але часто призводить до складних обчислень при великих значеннях коефіцієнтів при невідомому. Цей спосіб застосовують найчастіше, якщо хоча 6 при одному з невідомих коефіцієнт дорівнює 1 або -1.
3. Спосіб алгебраїчного додавання часто використовується тоді, коли коефіцієнти при одному з невідомих чисельно рівні або їх можна звести до однакової числової величини в рівносильному рівнянні без складних обчислень.
Спосіб підстановки
Означення. Спосіб підстановки полягає в тому, що з кожного рівняння одне з невідомих виражається через друге невідоме, і так доти, доки не одержимо результуюче рівняння, у якому буде лише одне невідоме.
Визначивши невідоме в результуючому рівнянні, ми у зворотному порядку, ідучи від рівняння до рівняння, знаходимо всі невідомі.
Для системи рівнянь з двома невідомими підстановку проводять лише один раз.
Наприклад задані системи рівнянь розв’язати способом підстановки.
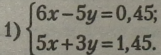
|
Розділимо всі одночлени другого рівняння на 5: |
 |
|
Визначимо х через у, склавши і розв’язавши рівняння відносно дг. |
 |
|
Підставимо одержане значення х у перше рівняння системи і розв’яжемо його, визначивши числове значення і/*. |
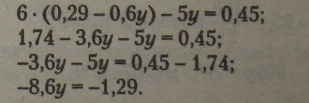 |
|
Помножимо ліву і праву частину рівнянь на (-1): |
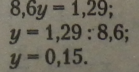
|
Підставимо знайдене значення у у рівняння (*): |
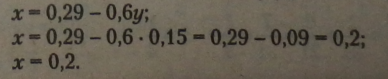 |
Зведемо всі одночлени до спільного знаменника і знаменник відкинемо. В обох рівняннях спільний знаменник 21.
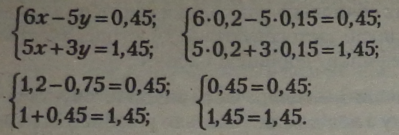 |
|
Розв’язання правильне, оскільки дістали тотожності. Відповідь:* - 0,2; у «= 0,15. |
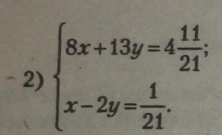
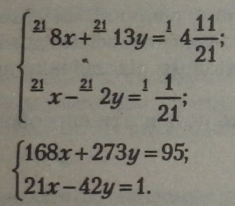
|
Ця система рівнянь рівносильна заданій. У другому рівнянні системи виразимо * через у \ |
 |
|
Підставимо одержане значення * у перше рівняння системи і розв’яжемо його, визначивши числове значення у\ |
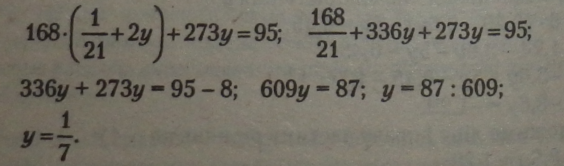 |
|
Підставимо знайдене значення у у рівняння (*): |
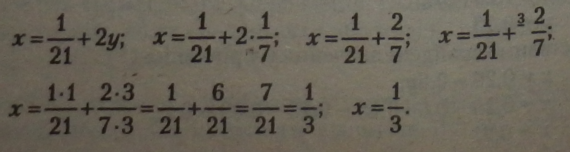 |
Спосіб алгебраїчного додавання
Означення. Спосіб алгебраїчного додавання полягає в одер-. жанні рівносильного рівняння з одного із заданих і додавання двох рівнянь, таким чином здійснюється перехід до одного рівняння з одним невідомим.
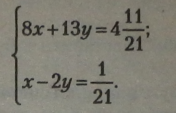
|
Підставимо значення змінних у вихідну систему, зведемо всі одночлени до спільного знаменника і знаменник відкинемо: |
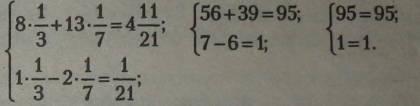 |
|
Розв’язання правильне, оскільки дістали тотожності. |
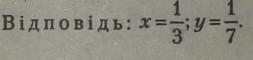
Цей спосіб розв’язання при одержанні рівносильного рівняння вимагає застосування однієї з основних властивостей рівнянь (множення або ділення на одне й те саме число всіх членів рівняння).
Приклади. Задані системи рівнянь розв’язати способом алгебраїчного додавання:
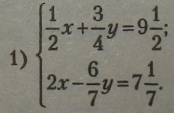
|
Помноживши всі одночлени першого рівняння на -4, дістанемо рівняння, рівносильне заданому: |
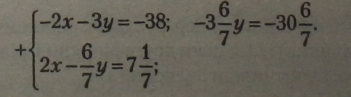 |
|
Помножимо обидві частини рівності на (-1): |
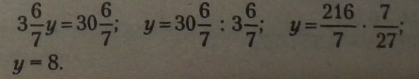 |
не рівносильне першому рівнянню системи, це рівняння суми.
Одержане значення невідомого у можна підставити в будь-яке із заданих рівнянь системи.
|
Рівняння |
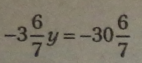 |
Підставивши одержане значення у у друге рівняння системи, дістанемо рівняння, рівносильне заданому, і розв’яжемо його, визначивши невідоме значення хг.
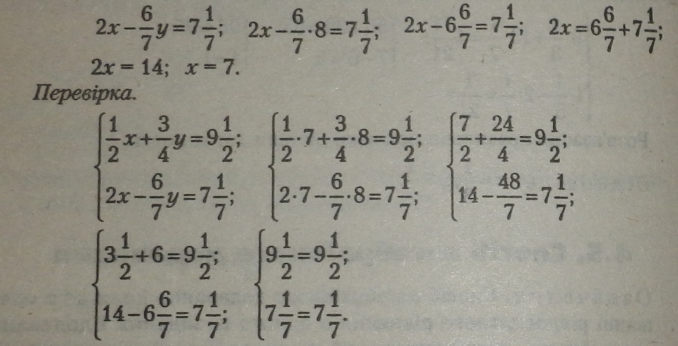 |
|
Розв’язання правильне, оскільки дістали тотожності. Відповідь:лг = 7;у = 8. |
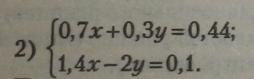
Помноживши всі одночлени першого рівняння на -2, дістанемо рівняння, рівносильне заданому:
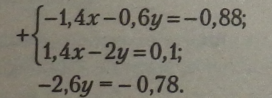 |
|
Помножимо обидві частини рівності на -1: |
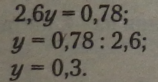
Підставивши знайдене значення у у перше задане рівняння системи (можна в будь-яке з двох рівнянь) і діставши друге рівняння, рівносильне заданому, розв'яжемо його, визначивши значення*:
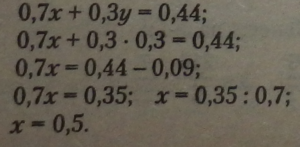
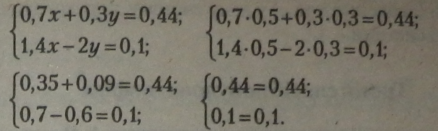 |
|
Розв’язання правильне, оскільки дістали тотожності. Від повідь:*-0,5; у-ОД |
Графічне розв'язування системи рівнянь
Означення. Графічний спосіб розв’язування системи рівнянь з двома невідомими передбачає побудову графіків двох рівнянь в одній плоскій системі координат. Координати точок перетину графіків будуть розв’язками системи рівнянь (перевірка обов’язкова).
Перший спосіб побудови графіка
І. Звести рівняння з двома невідомими ах+by = с до рівносильного рівняння типу у =рх+ q. Для цього в рівнянні одночлен ах переноситься у праву частину рівняння з протилежним знаком і обчислюється числове значення коефіцієнтів рівносильного рівняння:
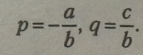
2. Щоб побудувати графік рівняння, треба побудувати пряму за двома точками (одна з яких — точка початку координат) рівняння прямої пропорційності у=рха потім цю пряму при q>0 паралельно перенести вгору по осі ординат на значення модуля коефіцієнта q, або при q < 0 паралельно перенести вниз по осі ординат на значення модуля коефіцієнта q.
3. Знайти координати точок перетину графіків. Підставляючи знайдені координати (знайти х та у) у дану систему, переконатися, що вони є розв’язком цієї системи.
Другий спосіб побудови графіка
1. За кожним рівнянням ах+by - с визначити дві точки на координатній площині, які належать графіку рівняння, надавши довільне числове значення одному невідомому (х або у) і обчисливши за ним друге невідоме.
2. Через обчислені дві точки кожного рівняння провести прямі — графіки рівнянь.
3. Знайти координати точок перетину графіків. Підставляючи знайдені координати (значення х та у) у дану систему, переконатися, що вони є розв'язком цієї системи.
Третій спосіб побудови графіка
Він відрізняється від другого тільки пунктом 1. Визначення точок на графіку рівнянь здійснюється у точках перетину графіків з осями координат (перша точка має х ■= 0, а друга — у ~ 0).
Правило. Графічним розв'язком системи двох рівнянь з двома невідомими є координати точок перетину графіків заданих рівнянь.
При розв'язанні систем лінійних рівнянь графічним способом перевірка обов'язкова!
Приклади.
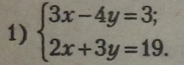
Виділимо невідоме у з рівнянь, створивши рівносильні рівняння.
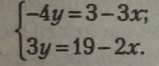
Помножимо перше рівняння на (-1), створивши рівносильні рівняння:
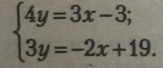
Виділимо у з кожного рівняння, створивши рівносильні рівняння.
Складемо рівносильні рівняння виду у=*ах+Ь. Графічне розв’язування цих рівнянь зводиться до побудови графіка прямої пропорційності у — ах> з його подальшим паралельним перенесенням по осі ординат вгору на Ь одиниць, якщо Ь > 0, і вниз на |6| одиниць, якщо b < 0.
|
Графіки рівнянь |
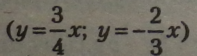 |
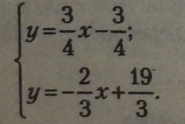
проходять через точку початку
координат (0; 0). Для побудови цих графіків (прямих) потрібно ще визначити по одній точці для кожного рівняння.
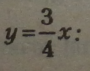
Для першого допоміжного графіка
Координати точок на допоміжному графіку першого рівняння: О (0; 0)іЛ (4; 3).
Для другого допоміжного графіка
Нехай х - 4, тоді, підставивши значення абсциси в рівняння, обчислимо значення ординати:
Нехай х - 3, тоді, підставивши значення абсциси в рівняння, обчислимо значення ординати:
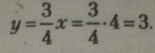
Координати точок на допоміжному графіку другого рівняння: О (0; 0) і В (3; -2).
Побудуємо допоміжні графіки (пунктирними лініями на малтоккуУ Перший одержаний графік перенесемо паралельно на
Перевіркою переконуємось, що точка перетину одержаних графіків К (5; 3) є розв’язком даної системи рівнянь.
Відповідь: x = 5; у = 3.
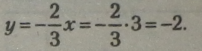
Зведемо рівняння до спільного знаменника, створивши рівносильні рівняння:
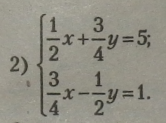
Виділимо одночлен зі змінною у у рівняннях, створивши рівносильні рівняння:
Створимо нові рівносильні рівняння без дробів:
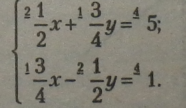
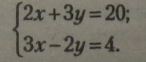
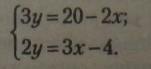
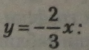
 |
одиниці |
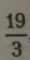 |
, або |
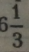 |
одиниці. |
вниз по осі ординат, а другий — паралельно вгору на
Виділимо змінну у з кожного рівняння, створивши рівносиль^ рівняння:
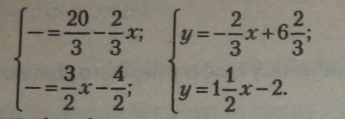
Щоб побудувати графіки рівнянь, обчислимо по дві точки дд» кожного графіка, склавши таблицю.

За парою точок (А і В; С і Д) побудуємо графіки рівнянь. Перевіркою переконуємося, що точка перетину двох графіків К (4; 4) є розв’язком системи рівнянь.
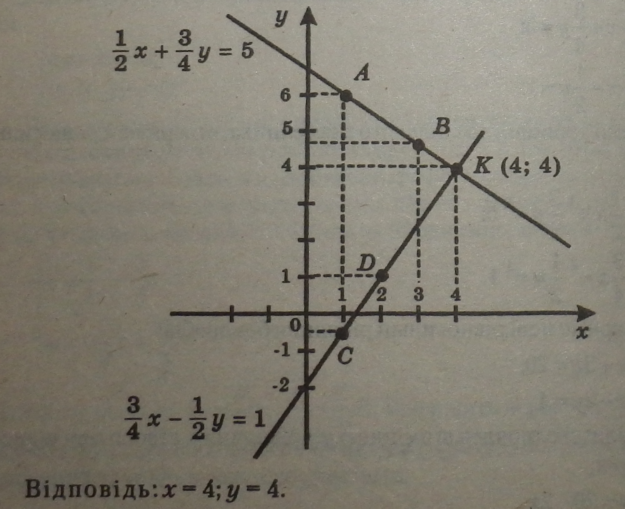
Графічне розв'язування системи лінійних рівнянь можна перевіри* ти алгебраїчно. Для цього треба розв’язати алгебраїчно систему рівнянь»
при правильній графічній побудові корені рівнянь дорівнюють координатам точки перетину графіків.
Наприклад, перевіримо останню побудову графіків.
Алгебраїчна перевірка завдання 2.
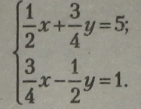
Зведемо рівняння до рівносильних рівнянь:
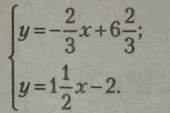
|
Оскільки ліві частини рівнянь системи рівні (у - у), то і праві частини рівнянь також рівні. |
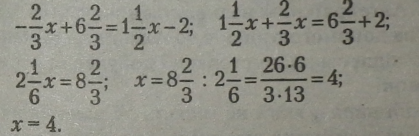 |
|
Підставимо у будь-яке рівняння значення х=4: |
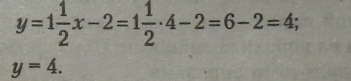 |
|
Оскільки координати точки К і алгебраїчний розв’язок рівнянь збігаються, то координати точки К визначені правильно. |
Таким же чином можна, не розв’язуючи систему рівнянь графічно, знайти координати точки перетину графіків алгебраїчно і схематично побудувати графіки рівнянь.
Якщо в рівносильному рівнянні у — ох + Ь\
— коефіцієнт а > 0, то графік рівняння проходить через І і III квадранти (нахилений вправо);
— коефіцієнт а < 0, то графік рівняння проходить через II і IV квадранти (нахилений вліво);
— чим більше значення а, тим ближче нахилений графік до осі ординат, чим менше значення а — тим ближчий нахил графіка до осі абсцис;
— при b > 0 — графік перенесений вгору по осі у на |Ь| одиниць, у порівнянні з графіком прямої пропорційності, при | < 0 — графік перенесений вниз по осі у на \Ь\ одиниць.
Автор: admin от 8-06-2013, 22:20, Переглядів: 35802