Розкладання многочленів на множники - винесення спільного множника за дужки, спосіб групування
Винесення спільного множника за дужки
Означення. Розкласти многочлен на множники — це означає виразити многочлен у вигляді добутку одночлена на многочлен або добутку двох та більше многочленів, який тотожний заданому многочлену.
Розкладання многочленів на множники можливе при винесенні спільного множника за дужки, або групуванням кількох одночленів многочлена з наступним одержанням добутку многочленів, або заміною многочлена добутком за допомогою формул скороченого множення.
Правило. Щоб винести спільний множник за дужки, треба кожний член многочлена поділити на спільний множник і дальние взяти одним із множників добутку, а другим множником добутку буде многочлен, складений із часток.
|
Приклади. |
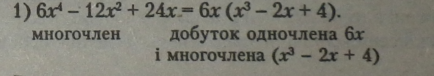 |
Розкласти многочлен на множники винесенням спільного множника за дужки можливо тоді, коли такий множник є в кожному члені многочлена.
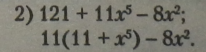
Цей многочлен не можна розкласти на множники, оскільки У тричлена немає спільного дільника (множника II). Після винесенні спільного множника 11 з двох перших доданків подальше спрощення неможливе.
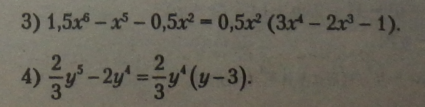
Спосіб групування
Правило. Спосіб групування передбачає переведення многочлена у тотожний заданому многочлену добуток многочленів.
Із кількох одночленів, об’єднавши їх у групи (многочлени в многочлени), треба винести спільний множник для кожної групи, а многочлени 4Із остач* (часток) будуть однаковими.
Однакові многочлени-множники в групах складуть спільний множник для заданого многочлена. Його записують першим множником добутку.
«Остачі», або частки (спільні множники для кожної групи многочленів), треба записати многочленом — другим множником добутку.
|
Приклади. |
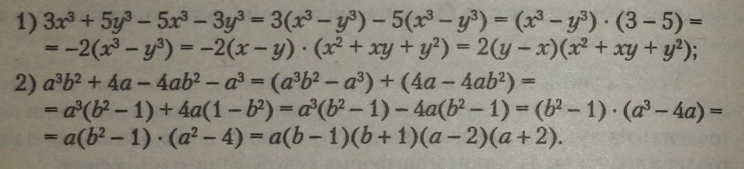 |
Використання формул скороченого множення
Попередня оцінка многочлена повинна показати, що заданий многочлен подібний до многочлена однієї з формул скороченого множення. Заданий многочлен може відразу являти многочлен формули (навіть якщо одночлени зображені алгебраїчними виразами) або вимагає перетворень (групування, винесення спільного множника, зведення подібних одночленів).
Правило. За формулами скороченого множення не кожен многочлен можна перевести в добуток, а тільки ті многочлени, які після всіх перетворень повністю відповідають многочлену формули.
|
Приклади. Многочлени, які розкладаються на множники за формулами: |
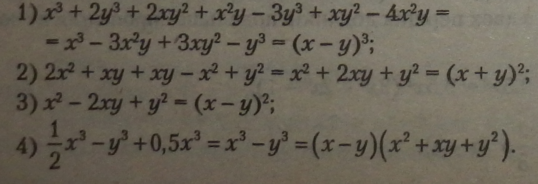 |
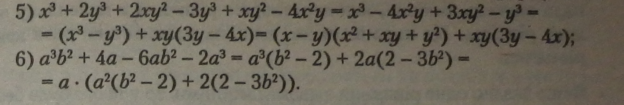
Різниця і сума кубів двох виразів
Формули різниці і суми кубів можна зобразити у многочлені так, що кожний член многочлена буде алгебраїчним виразом.
Обчислення за формулами скороченого множення зводиться до запису членів многочлена у вигляді виразів і подальшого їх перетворення як двох множників-многочленів (розкрити дужки, звести подібні члени в кожному многочлені), зберігаючи добуток.
Правило. Різниця і сума кубів двох виразів за формулами скороченого множення перетворюється на добуток двох многочленів або на добуток многочлена на одночлен.
|
Приклади. |
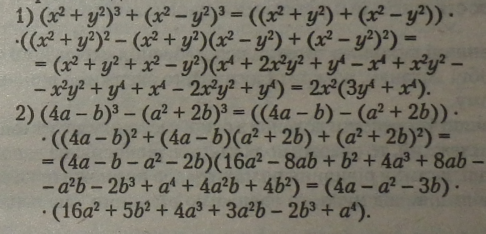 |
Автор: admin от 8-06-2013, 22:13, Переглядів: 21089