Многочлен, додавання і віднімання многочленів, множення многочленів
Многочлен
Означення. Многочленом називається сума кількох одночленів.
Кожний одночлен у многочлені називається членом многочлена.
Подібні доданки називаються подібними членами многочлена, а зведення подібних доданків — зведенням подібних членів многочлена. Многочлен, який складається із стандартних одночленів, упорядкованих за спадними степенями, серед яких немає подібних, називається многочленом стандартного вигляду.
Одночлен найбільшого степеня стандартного вигляду визначає степінь многочлена.
Приклад.
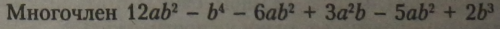
складається з 6 одночленів стандартного вигляду.
Многочлен четвертого степеня: степінь визначається одночленом найбільшого степеня (Ь4).
Многочлен має подібні членп.

|
Перетворимо многочлен, звівши подібні члени многочлена: |
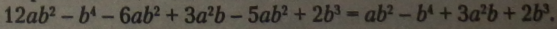 |
|
Впорядкуємо за спадними степенями букви Ь: |
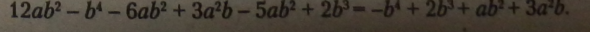 |
|
Результат обчислення |
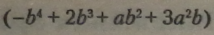 |
— чотиричлен четвертого степеня стандартного вигляду.
Додавання і віднімання многочленів
Правило. Щоб додати (відняти) два многочлени, треба записати їж поряд» сполучивши знаком + (або відповідно - ).
Порядок додавання многочленів
1. Записати всі многочлени як суму (один за одним через знак <+>).
2. Розкрити всі дужки (якщо перед многочленом стоїть знак +, то всі його члени записуються зі своїми знаками, якщо стоїть знак «-», то всі члени многочлена змінюють свої знаки на протилежні).
3. Звести подібні члени многочлена суми. Підкреслити однакові одночлени і додати їх коефіцієнти.
|
Приклад. Додати многочлени: |
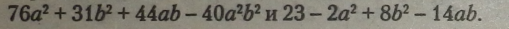 |
|
Запишемо многочлени як доданки (зі знаком «+*• між нйми): |
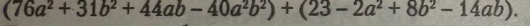 |
|
Підкреслимо подібні члени многочлена і додамо їх коефіцієнти: |
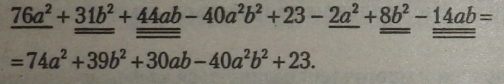 |
|
Результатом обчислень суми многочленів став також многочлен, який складається з 5 одночленів. |
Порядок віднімання многочленів
1. Записати всі многочлени як різницю першого многочлена—зменшуваного — і другого многочлена — від’ємника (через знак «-», взявши другий многочлен у дужки).
2. Розкрити всі дужки (якщо перед многочленом стоїть знак "-", то всі члени многочлена змінюють свої знаки на протилежні).
3. Звести подібні члени многочлена (підкреслити однакові члени і додати їх Коефіцієнти).
|
Приклад. Відняти многочлени (перший многочлен — зменшуване, а другий — від’ємник). |
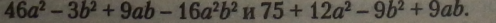 |
|
Запишемо многочлени як різницю (зі знаком <г-> перед другим многочленом, взятим у круглі дужки): |
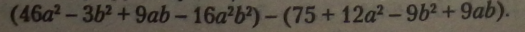 |
|
Розкриємо дужки, змінивши перед одночленами в дужках знаки на ппотилежні: |
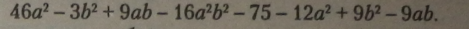 |
|
Підкреслимо подібні члени многочлена і додамо їх коефіцієнти: |
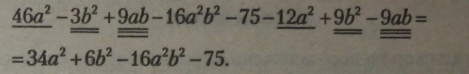 |
|
Результатом обчислень різниці многочленів став також многочлен, який складається з 4 одночленів. |
Множення многочленів
Многочлен множиться на одночлен, і многочлени перемножуються між собою. Обидва правила подібні до правила множення числа на вираз і множення двох виразів. Правила множення одночленів нам також відомі Оскільки одночлен і многочлен — раціональні вирази, то при їх множенні треба враховувати знаки одночленів (правила знаків при множенні).
Правило. Щоб помножити одночлен на многочлен, треба помножити цей одночлен на кожний член многочлена й додати одержані добутки.
|
Приклад як перемножити одночлен і многочлен: |
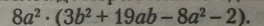 |
|
Записати добуток кожного одночлена на одночлен, визначивши знаки добутків: |
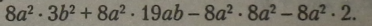 |
|
Перемножити кожну пару множників і взяти їх доданками, зберігаючи знаки попереднього обчислення: |
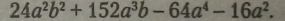
Оскільки подібних членів в одержаному' многочлені немає, то обчислення завершене.
Правило. Щоб помножити многочлен на многочлен, треба кожний член першого многочлена помножити на кожний член другого многочлена і отримані добутки додати.
Приклад.
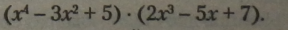
|
Помножити кожний член першого многочлена на кожний член другого многочлена із врахуванням знаків: |
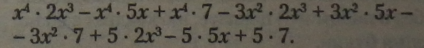 |
|
Перемножити кожну пару множників і зберегти знаки добутків, подібні члени підкреслити: |
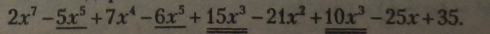 |
|
Звівши подібні члени, одержуємо: |
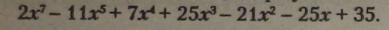 |
Автор: admin от 8-06-2013, 17:02, Переглядів: 20946