Нерівності: як розв'язувати нерівності з однією змінною

1°, Нерівності з однією змінною мають вигляд:

Розв'язком нерівності називається множина значень змінної, при яких дана нерівність буде правильною числовою нерівністю.

Дві нерівності називаються рівносильними, якщо множини їхніх розв'язків збігаються.

Основна ідея розв’язування нерівності полягає в заміні нерівності більш простою, але рівносильною заданій.

2°. При розв’язуванні нерівності використовують такі правила перетворення нерівності в рівносильну:

а) будь-який член нерівності можна перенести з однієї її частини в іншу з протилежним знаком, залишивши при цьому без зміни знак нерівності;

6) обидві частини нерівності можна помножити або поділити на одне й те саме додатне число, залишивши при цьому без зміни знак нерівності;

в) обидві частини нерівності можна помножити або поділити на одне і те саме від'ємне число, змінивши при цьому знак нерівності на протилежний;

г) якщо для одних і тих самих значень X справедливі нерівності f(x)>0, g(x)>0 i f(x)>g(x), то для тих самих значень виконується нерівність (f(x))ⁿ>(g(x))ⁿ, n є N.

3°. Нехай задана нерівність має вигляд f(x)/g(x)>0 (замість знака > можуть бути знаки <, >=, =<, а функція в знаменнику може бути сталою) або вона приведена до цього вигляду за допомогою правил вказівки 2.

Для розв'язування нерівності застосовується метод інтервалів (метод проміжків), який полягає в тому, що:

а) на числову вісь наносять точки х₁,x₂, х_n, що розбивають її на проміжки, в яких вираз f(x)/g(x) визначено і зберігає знак (плюс або мінус). Такими точками можуть бути корені рівнянь f(x)=0 і g(x)=0. Відповідні цим кореням точки позначають на числовій осі: зафарбованими кружками — точки, що задовольняють задану нерівність, світлими кружками — точки, що не задовольняють її;

б) відшукують і позначають на числовій осі знак виразу f(x)/g(x)  для значень х, які належать кожному з одержаних проміжків. Якщо функції f(x) і g(x) є многочленами і не містять множників виду (х-а)²ⁿ, де n є N, то достатньо визначити знак функції f(x)/g(x) в будь-якому такому проміжку, а в решті проміжків знаки плюс і мінус будуть чергуватися.

Якщо ж у чисельнику і знаменнику дробу f(x)/g(x) є множник виду (х-а)²ⁿ, де n є N, то покладаючи х ≠ а ділять обидві чістини заданої нерівності на множник (х-а)²ⁿ, додатний при всіх значеннях х ≠ а (див. вказівку 2°), і безпосередньою перевіркою з'ясовують, чи задовольняє значення х = а задану нерівність.

Приклад 1. Розв’язати нерівність

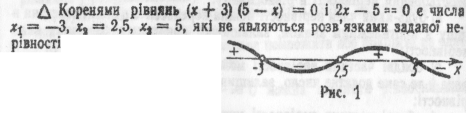
тому на числовій осі позначаємо їх світлими кружками (рис. 1). Ці точки розбивають числову вісь на чотири проміжки. Легко визначаємо, що при х>5 ліва частина нерівності від’ємна — ставимо знак мінус праворуч від точки 5 і, рухаючись вліво, чергуємо знаки плюс і мінус. При цьому зміну знаків зручно ілюструвати за допомогою хвилеподібної кривої (кривої знаків), проведеної через помічені точки і розміщеної вище або нижче від числової осі в відповідності із знаком нерівності в розглядуваному проміжку. За допомогою рис.1 дістаємо відповідь: (—∞; —3)U(2,5;5).

Це матеріал із довідника "Фізика 9 клас"