Розділ 3. Закон збереження енергії. Тема 1: Робота, потужність, енергія.
1.1 Робота. Потужність. Енергія.
 Робота — склярна величина, язеа є мірою механічної дії сили під час переміщення точки її прикладання.
Робота — склярна величина, язеа є мірою механічної дії сили під час переміщення точки її прикладання.
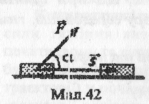
Робота сталої сили дорівнює добутку модуля сили F, модуля переміщення S і косинуса кута альфа між F та S (мал.42):
А = FScosα
Одиниця роботи — джоуль: 1 Дж = 1Н*м.
1 Джоуль дорівнює роботі, яку виконує сила в 1 Ньютон під час переміщення тіла на 1 метр, якщо її напрям збігається з напрямом руху.
Потужністю називається склярна величина, що дорівнює відношенню виконаної роботи до інтервалу часу, протягом якого вона була виконана:
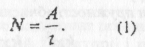
Потужність — величина, яка показує кількість роботи, що виконується за одиницю часу. Одиниця потужності в СІ — ват (Вт):
1 Вт = 1 Дж/с. 1 Вт — це потужність, при якій за 1 секунду виконуєтеся робота в 1 Джоуль.
Згідно з формулою (1) роботу можна визначити, якщо відома потужність N механізму, що її виконує, і час виконання

Ця формула дає можливість увести ще одну одиницю роботи, а отже і енергії — ват*секунду (Вт*с): 1 Вт*с= 1 Дж. Часто зустрічається значно більша одиниця роботи і енергії кіловат*година (кВт*год): 1 кВт*год=3,6*106 Дж.
Якшо під дією сталої сили тяги F тіло рухається рівномірно зі швидкістю ϑ то потужність дорівнює:
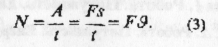
Під час руху автомобіля зі сталою швидкістю його сила тяги рівна за модулем силі опору. Тому з формули N=Fϑ видно, шо за сталої сили опору швидкість транспортного засобу прямо пропорційна потужності двигуна.
Із формули N=Fϑ видно також, що при сталій потужності двигуна чим менша сила опору середовища, тим більша швидкість транспортного засобу;
Робота сил тяжіння, пружності та тертя.
Робота сили тяжіння обчислюється за формулою:
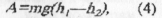
де h1—h2 — різниця висот у початковому та кінцевому положеннях.
Під час руху вниз робота сили тяжіння додатна (мал.43 а), під час руху вгору — від’ємна, (мал.44 б).
Робота сили пружності обчислюється за формулою:
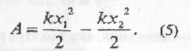
де к— жорсткість; х1, х2— початкова та кінцева координати вільного кінця деформованої пружини (коли початок координатної осі ОХ збігається з вільним кінцем недеформованої пружини, як це показано на мал.44.)
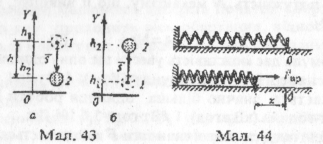
Якщо тіло повертається до по ложення рівноваги, значення деформації зменшується |x2|<|x1| при цьому відповідно до (5) робота сита пружності додатна. Якщо ж недеформоване тіло розтягуєтеся або стискається, то |x2|>|x1| і робота від’ємна.
Роботи сили тертя завжди від’ємна, оскільки під час руху сила тертя спрямована в бік, протилежний переміщенню:
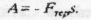
де Fтер— модуль сили тертя, S — модуль переміщення.
Консервативні сили.
У відповідності з формулою (4) робота сили тяжіння визначається тільки різницею висот у початковому та кінцевому положеннях. Якщо після спуску по будь-якій траєкторії тіло повертається (також по будь-якій траєкторії) у початкову точку, то робота на такій замкненій траєкторії дорівнює нулю. Щодо роботи сил пружності, то вона, у відповідності з (5), також визначається лише початковим і кінцевим положенням пружини. Під час розтягу (стиску) пружини і повернення у вихідне положення в формулі (5) x1=x2, отже A=0.
Таким чином, якщо тіло під дією сил тяжіння або пружності переміщується по замкнутій траєкторії і повертається в початкове положення, робота дорівнює нулю. Сили, які мають таку властивість, називаються консервативними. Сили тяжіння та пружності — консервативні сили. Сили тертя — неконсервативні, їхня робота на замкнутій траєкторії ніколи не дорівнює нулю.
Механічна енергія.
Енергією називають загальну кількісну міру руху і взаємодії всіх видів матерії. У фізиці розглядають різні форми енергії: механічну, внутрішню, хімічну, електромагнітну, гравітаційну, ядерну тощо.
Зміна енергії завжди пов’язана з виконанням роботи, тому кажуть, що енергія — це величина, що вказує на здатність виконувати роботу. Енергію позначають літерами Е або W і вимірюють, як і роботу, у джоулях.
Зміна енергії завжди дорівнює виконаній роботі:
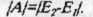
Кінетична енергія.
Знайдемо роботу, яку виконує стала сила F по переміщенню тіла масою m на відстань S по гладенькій горизонтальній площині. Якшо напрям сили збігається з напрямом переміщення, а початкова швидкість тіла дорівнює нулю, тоді з кінематичної формули
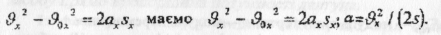
Робота сили дорівнює:
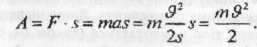
Склярну величину mϑ2/2, яка має розмірність роботи, називають кінетичною енергією. Кажуть, що за рахунок виконаної над тілом роботи воно досягає певної швидкості і набуває кінетичної енергії. Отже, кінетичною енергією тіла масою m, що рухається у даній інерціальній системі координат
зі швидкістю ϑ, кінетична енергія дорівнює
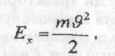
У різних системах відліку швидкості одного й того самого тіла в даний момент часу можуть бути різними. Отже, кінетична енергія — величина відносна, вона залежить від вибору системи відліку.
Якщо на тіло під час руху діє сила (або одночасно кілька сил), кінетична енергія тіла змінюється — тіло прискорюється або зупиняється. При цьому робота сили або рівнодійної сил, прикладених до тіла; дорівнює зміні кінетичної енергії тіла:
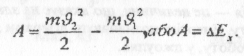
Останнє твердження і формула, що його виражає, називається теоремою про кінетичну енергію.
Потенціальна енергія.
Потенціальна енергія — це енергія взаємодії тіл, що залежить від взаємного розміщення тіл або частин одного й того самого тіла (тіло, підняте над Землею, розтягнена або стиснена пружина, стиснений газ тощо). Наведемо приклади.
Потенціальна енергія тіла масою m, піднятого на висоту h над Землею, дорівнює
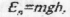
де g - прискорення вільного падіння. Ця формула справедлива, якщо поверхню Землі вважати за нульовий рівень відліку енергії і обчислювати енергією на висотах h, значно менших радіуса Землі: h << Rземлі.
Тепер формулу (4), що визначає роботу сил тяжіння, можна подати у такому вигляді:
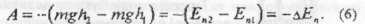
Отже, робота сил тяжіння дорівнює зміні потенціальної енергії тіла, взятій з протилежним знаком.
Потенціальна енергія деформованої пружини:
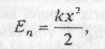
де k — жорсткість, х — видовження (стиснення).
Тепер формулу (5), що визначає роботу сил пружності, можна подати у вигляді:
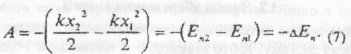
Отже, робота сил пружності дорівннює зміні потенціальної енергії пружно деформованого тіла, взятій з протилежнім знаком.
Підкреслимо, що потенціальна енергія - це енергія взаемодї тіл. Не має фізичного змісту поняття "потенціальна енергія одного тіла" (якщо, звичайно, не йдеться про деформоване тіло, але й тоді мається на увазі енергія взаємного розташування частин тіла, які тут виступають як окремі тіла). Коли йдеться про потенціальну енергію тіла, піднятого на висоту, мається на увазі, що тіло взаємодіє із Землею, і енергію має система “тіло-Земля”. Коли йдеться про потенціальну енергію деформованої пружини, мається на увазі, що атоми у пружно деформованому тілі зміщені віл положень рівноваги і між сусідніми атомами переважають сили взаємного притягання або відштовхування.
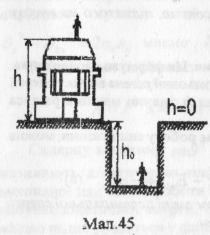
Відносний характер потенціальної енергії. Залежно від вибору системи відліку і нульового рівня потенціальна енергія може бути як додатною, так і від’ємною величиною. Цс ілюструє мал.45, на якому зображено дві людини — одну на даху будинка, другу — на дні котловану. Відносно поверхні Землі потенціальна енергія першої людини додатна (mgh), а другої — від'ємна (-mgh0). У той самий час відносно дна котловану потенціальна енергія першої людини дорівнює mg(h +h0), другої — нулю. Отже, потенціальна енергія тіла різна в різних системах відліку, тобто є відносною величиною.
1.2. Закон збереження енергії.
Розглянемо питання про взаємодію двох тіл, що складають замкнену систему, тобто взаємодіють тільки одне з одним.
У попередніх параграфах ми встановили, що коли тіла взаємодіють одне з одним силами пружності або тяжіння, виконана цими силами робота дорівнює взятій з протилежним знаком зміні потенціальної енергії тіл системами:
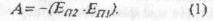
Разом з тим, за теоремою про кінетичну енергію, ця сама робота дорівнює зміні кінетичної енергії:

Порівнюючи (1) та (2), можна записати:
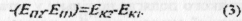
Бачимо, що на скільки зменшується потенціальна енергія, на стільки й збільшується кінетична. Все відбувається так, ніби один вид енергії перетворюється в інший. Формулу (3) можна переписати так:
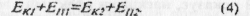
Отже, сума кінетичної і потенціальної енергії тіл, які складають замкнену систему ї взаємодіють між собою силами тяжіння та силами пружності, залишається незмінною у будь-який момент часу, тобто зберігається. Це твердження і называеться законом збереження енергії в механічних процесах.
Сума кінетичної та потенціальної енергії тіл називається повною механічною енергією. Для повної механічної енергії закон збереження енергії формулюється так:
у будь-який момент часу полна механічна енергія замкненої системи тіл, взаемодіючих силами тяжіння та пружності, залишається сталою (зберігається):
Еповн=Eк+Eп=const
Закон збереження енергії розкриває фізичний зміст поняття роботи. Той факт, що та сама робота спричиняє збільшення кінетичної або те ж саме зменшення потенціальної енергії, означає, що робота дорівнює енергії, яка перетворилися з одного виду в інший.
Робота сили тертя і механічна енергія.
Якщо в системі разом із силами тяжіння і пружності діють сили тертя або опору, повна механічна енергія зменшується. Внутрішня ж енергія взаємодіючих тіл при цьому збільшується, про що свідчить, наприклад, нагрівання тіл. Зменшення механічної енергії точно дорівнює збільшенню внутрішньої.
Отже, в загальному випадку, справедливий закон збереження повної енергії в природі:
енергія не виникає та не зникає, а тільки передається від одного тіла до іншого, або перетворюється з одного виду в інший в еквівалентних кількостях.
Закон збереження енергії — це фундаментальний закон природи, зміст якого полягає не тільки у встановленні факту збереження повної енергії, але й у розумінні можливості взаємних перетворень різних видів енергії.
Коефіцієнт корисної дії (ККД).
Кожна машина, кожний двигун характеризується коефіцієнтом корисної дії (скорочено ККД), який показує, наскільки ефективно використовується енергія, шо проводиться до машини. Коефіцієнт корисної дії дорівнює відношенню корисної роботи Ак, яка виконується машиною, до всієї виконаної (повної) роботи Апов:
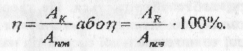
Оскільки А =Nt, то можна записати:
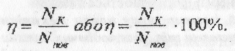
де Nk — корисна, а Nпов — повна потужність.
1.3 Робота під дією сталої і змінної сил.
Сила є функцією координати. Якщо сила стала, то вона не залежить від координати. Це, наприклад, сила F=mg, F=const. Сила пружності лінійно залежить від координати F=kx, а сила всесвітнього тяжіння — обернено пропорційна квадратові координати:
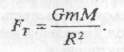
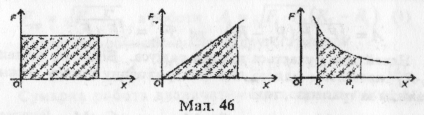
Побудуємо графік залежностей цих сил від координати (мал. 46):
1. Коли на тіло діє сила F і тіло при цьому здійснює переміщення, то робота цієї сили дорівнює добугку модуля сили і переміщення A=F*x; (1).
Для сталої сили робота буде дорівнювати площі прямокутника, обмеженої графіком сили і осями координат.
2. Розглянемо випадок, коли сила змінюється за лінійним законом. Нехай це буде сила пружності F=kx. Оскільки робота визначається площею фігури обмеженою графіком сили і осями координат, то
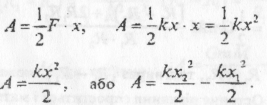
Висновок: Якщо сили лінійно залежать від координати, то робота визначається 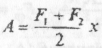 добутком середнього арифметичного сил на початку і в кінці переміщення.
добутком середнього арифметичного сил на початку і в кінці переміщення.
3. Робота гравітаційної сили.
Оскільки графіком залежності сили від координати є гіпербола, то роботу сили можна обчислити, знаючи площу криволінійної трапеції. В 10-11 класах можна роботу обчислити за допомогою інтегрального числення. Ми ж користуємось графічним методом і доведемо, що в такому разі роботу обчислюють добутком середнього геометричного крайніх значень сил на переміщення:
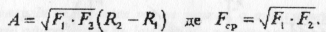
Нехай тіло рухається вздовж радіуса. Візьмемо віддаль R2-R1 наскільки малою, що заштриховану площу можна вважати за трапецію, тоді
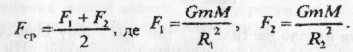
Отже,
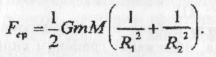
Перепишемо останню формулу в такому вигляді:
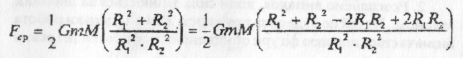
або
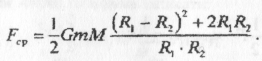
Оскільки R1 приблизно дорівнює R2, тоді вираз — (R1-R2)2 можна прийняти рівним нулю. Останнє рівняння спроститься і матиме вигляд:
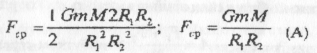
Праву частину рівняння (А) піднесемо до квадрату і добудемо квадратичний корінь:
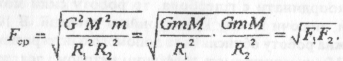
Звідси одержуємо вираз для відшукання середньої сили
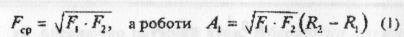
Аналогічно обчислимо площу другої трапеції
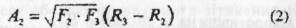
Сумарна робота визначатиметься сумою площ всіх трапецій.
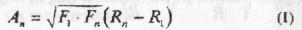
Висновок: Робота змінної центральної сили визначається добутком середнього геометричного крайніх значень сили на переміщення.
Пізніше значення роботи можна одержати застосувавши елементи вищої математики.
Використовуючи формулу (1), можна вивести формулу потенціальної енергії взаємодії тіла масою m з Землею М
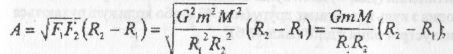
Розкривши дужки, пишемо:
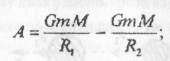
оскільки 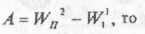
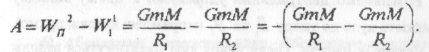
Тобто,
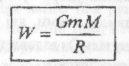
Знання залежності потенціальної енергії від R дає змогу обчислиш II космічну швидкість ракети. На основі закону збереження енергії:
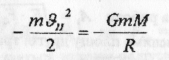
Скоротивши на m знайдемо ϑII:
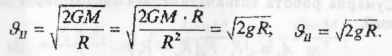
Оскільки
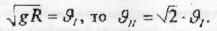
Друга космічна швидкість в 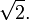 більша за першу космічну швидкість.
більша за першу космічну швидкість.
1.4. Пружний і непружний удари тіл.
Закони збереження імпульсу і енергії дають змогу вивчати зіткнення (удари) двох куль. Зіткнення може відбуватися, коли одна з куль наздоганяє другу (мал.47 а) або коли кулі рухаються назустріч одна одній (мал.47 б).
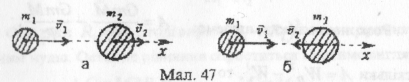
Розглянемо центральний удар куль. У цьому випадку швидкість куль до удару ϑ1 та ϑ2 напрямлені вздовж прямої, що з’єднує їх центри. Після удару кулі рухатимуться вздовж тієї самої прямої із швидкостями, які позначимо U1 та U2. Спрямуємо координатну вісь Ох вздовж цієї прямої і запишемо проекції швидкостей без індексу X:
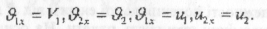
Розглянемо два граничних випадки ударів — абсолютно пружний і абсолютно непружний удар.
а). Абсолютно пружиний удар.
Абсолютно пружним називається такий удар, при якому повна механічна енергія тіл зберігається. Після абсолютно пружного зіткнення тіла розлітаються із швидкостями, які визначаються двома умовами — збереженням сумарної енергії і сумарного імпульсу. Закон збереження імпульсу для абсолютно пружного удару в проекціях на вісь Ох запишеться так:
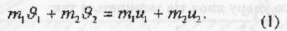
Значення проекцій швидкостей ϑ1 та ϑ2, U1 та U2 беруть із знаком плюс, якщо куля рухається в додатному напрямі осі ОХ, або із знаком мінус, якщо напрям руху протилежний.
Закон збереження механічної (кінетичної) енергії для абсолютно пружного удару матиме вигляд:
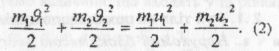
Розглядаючи (1) і (2) як систему двох рівнянь і розв'язуючи її відносно невідомих U1 та U2, знаходимо швидкості тіл після абсолютно пружного удару:
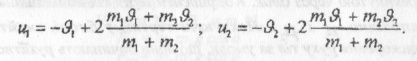
б). Абсолютно непружний удар.
Абсолютно непружним називається удар, після якого тіла рухаються з однаковими швидкостями (тобто як одне тіло) або знаходяться у стані спокою. При такому ударі виконується лише закон збереження імпульсу, закон же збереження енергії не виконується - механічна енергія повністю або частково переходить у внутрішню.
Для абсолютно непружного удару закон збереження імпульсу запишеться так:
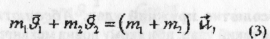
де U — швидкість тіл після удару. З (3) знаходимо що
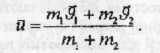
Закон збереження повної енергії для абсолютно непружного удару двох тіл запишеться так:
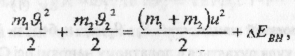
де ΔЕвн — енергія тіл, яка під час непружного удару перетворюється у внутрішню.
Це матеріал із довідника "Фізика 9 клас"
Автор: admin от 12-07-2014, 14:49, Переглядів: 36725