Тотожні перетворення раціональних виразів, раціональні рівняння
Тотожні перетворення раціональних виразів
Означення. Два і більше виразів, відповідні значення яких прн всіх допустимих значеннях змінних, що входять до них, рівні називаються тотожно рівними.
|
Приклади. |
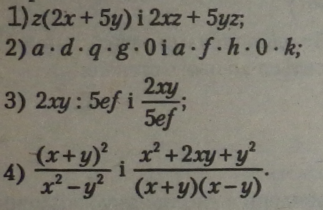 |
Тотожні перетворення виразів називають перетворенням виразів.
Часто у прикладах умова пропонує спроститивирази — це означає провести тотожні перетворення цих виразів, замінивши їх більш простими.
Означення. Рівність, правильна при всіх допустимих значеннях змінних, що входять до неї, називається тотожністю.
Довести тотожність — це означає виконати в лівій і правій части* нах рівності тотожні перетворення, у результаті яких в обох частинах будуть стояти однакові вирази.
Розкласти на множники — це означає тотожно перетворити вираз, у результаті чого многочлен у даному виразі замінюється на добуток многочленів або одночлена і многочлена.
Скоротити дріб—це означає тотожно перетворити дріб, щоб отримати більш простий вираз.
|
Приклади. 1. Дано раціональний вираз: |
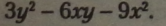 |
Потрібно перетворити многочлен у добуток.
|
Розв'язання. Подамо 3у2 різницею Ау2-у2 і перепишемо вираз. У трьох останніх одночленів виносимо за дужки знак |
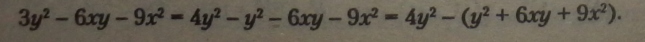 |
у дужках тричлен є квадратом двочлена (за формулами скороченого множення), який ми запишемо замість тричлена:
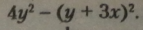
Застосуємо формулу різниці квадратів для перетворення різниці на добуток:
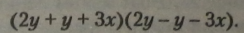
|
Зводимо подібні додатки у кожній дужці і виносимо спільний множник із першого множника за дужки: |
 |
|
Усі наведені нижче рівності — рівносильні. |
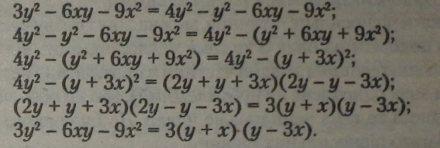 |
2. Перетворити на добуток раціональний вираз
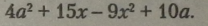 |
|
Розв’язання. |
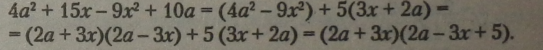
Многочлен перетворимо на суму двох многочленів і винесемо із другого многочлена спільний числовий множник.
У першому многочлені — формула різниці квадратів, яку замінимо на добуток. У суми двох многочленів з’явився однаковий двочлен, який можна винести як спільний множник за дужки.
|
3. Перетворити дробовий раціональний вираз (скоротити дріб): |
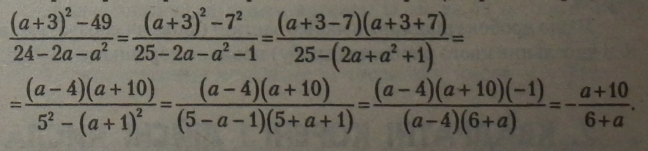 |
Раціональні рівняння
Рівняння — це рівність, що містить невідоме або невідомі, задані буквами.
Нехай с рівність 2 + 8-=4 + 6. Замінимо 2 на В (х 9 2) і складемо рівняння х + 8 " 2х + 6.
Щоб розв’язати це рівняння, потрібно знайти значеннях, тобто виконати обернену дію. І лише х- 2 може наше рівняння перетворити на рівність. Ніяке інше значення зрівняння на рівність не перетворить. Тому
х - 2 і є розв’язком нашого рівняння, або його коренем. Складання рів. няння за числовою рівністю і розв’язування рівняння — цеє взаємообер-нені перетворення двох виразів, з’єднаних знаком рівності.
Означення. Раціональним називається рівняння, ліва і права частини якого — раціональні вирази. Розв’язком раціонального рівняння називаються ті значення невідомого, які перетворюють це рівняння на правильну числову рівність.
Два і більше рівнянь, які мають однакові корені (однакові значення невідомого), називаються рівносильними рівняннями. Рівняння, які не мають коренів, також називаються рівносильними.
Щоб одержати рівносильне рівняння, можна ліву і праву частини його помножити або поділити на одне й те саме число, відмінне від нуля, або перенести одночлени рівняння з однієї частини в протилежну від знаку рівності (змінивши знак одночлена на протилежний), або до обох частин рівняння додати одне й те саме раціональне число. До будь-якого рівняння можна дібрати багато рівносильних рівнянь.
|
Приклади рівносильних рівнянь: |
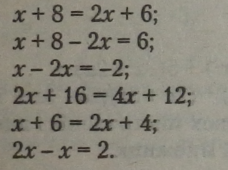 |
Степінь рівняння дорівнює найбільшому степеню його одночленів. Який степінь у рівнянні, стільки ж воно має коренів.
Раціональне рівняння називається дробовим рівнянням, якщо одна з його частин (ліва чи права) або обидві частини рівняння містять дробові вирази.
Якщо дробове рівняння в якійсь частині (зліва чи справа) має нуль, тоді чисельник цього рівняння (дробу) повинен дорівнювати нулю.
Автор: admin от 8-06-2013, 22:34, Переглядів: 12964