Формули скороченого множення

Формули скороченого множення призначені для скорочення обсягів обчислень, спрощення скорочення дробів у буквених виразах (многочлен можна перевести в добуток і навпаки — добуток у многочлен).

1. Формула квадрата суми двох виразів:

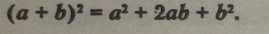Правило. Квадрат суми двох виразів дорівнює квадрату пер* шого виразу плюс подвоєний добуток першого виразу і другого, плюс квадрат другого виразу.

Приклади.

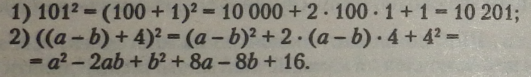У першому прикладі представлено тризначне число як сума двох розрядних одиниць, зручних для піднесення до квадрату.

У другому прикладі перший доданок є двочленом.

2. Формула квадрата різниці двох виразів:

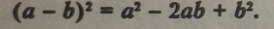Правило. Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток першого і другого виразів плюс квадрат другого виразу.

Приклади.

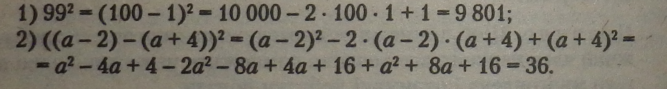У першому прикладі число замінено на різницю розрядних одиниць, зручних для піднесення до квадрату.

У другому прикладі маєкіо різницю двочленів, квадрат кожного можна замінити многочленом за формулами скороченого множення, далі при обчисленні застосовується зведення подібних доданків. Результат обчислень (число без невідомого) показує, що квадрат заданої різниці не залежить від значення букви.

3. Формула різниці квадратів двох виразів:

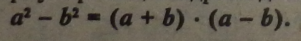Правило. Різниця квадратів двох виразів дорівнює добутку суми і різниці цих виразів.

Приклади.

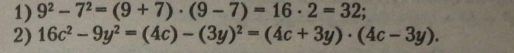У Другому прикладі коефіцієнти при квадратах двочлена треба розглядати як квадрати чисел, тобто як добуток алгебраїчних множників.

Отже, вирази у формулі — це одночлени 4с і 3у. Знак різниці квадратних двочленів визначається за множником з різницею, а не з сумою, оскільки в сумі доданки можна міняти місцями, а в різниці ні. Вираз 16с² - 9у² не дорівнює виразу 9у¹- 16с².

4. Формула куба суми двох виразів:

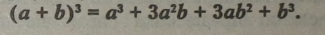Правило. Куб суми двох виразів дорівнює кубу першого ви* разу плюс потроєний добуток квадрата першого і другого виразів плюс потроєний добуток першого виразу і квадрата другого виразу плюс куб другого виразу.

Щоб одержати формулу куба суми двох виразів, можна перемножити квадрат суми і суму тих самих виразів:

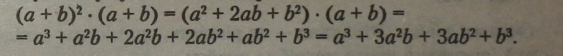Приклад.

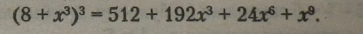5. Формула куба різниці двох виразів:

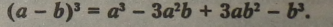Правило. Куб різниці двох виразів дорівнює кубу першого виразу мінус потроєний добуток квадрата першого і другого виразів плюс потроєний добуток першого і квадрата другого виразів мінус куб другого виразу.

Щоб одержати формулу куба різниці двох виразів, можна перемножити квадрат різниці і різницю тих самих виразів:

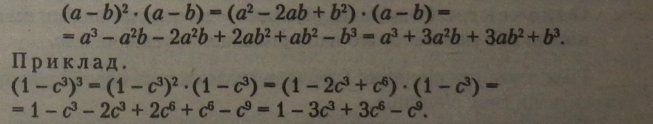6. Формула різниці кубів двох виразів:

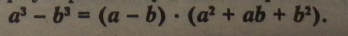7. Формула суми кубів двох виразів:

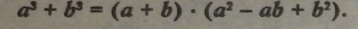Правило. Сума кубів двох виразів дорівнює добутку суми цих виразів І неповного квадрата їх різниці.

Правило. Різниця кубів двох виразів дорівнює добутку різниці цих виразів і неповного квадрата їх суми.